标准偏差怎么算？详解标准差计算方法及应用场景

本文详细介绍了标准偏差的计算方法、应用场景以及需要注意的误区。文章从样本标准差、总体标准差以及分组数据等不同角度阐述了标准偏差的计算，并指出了在实际应用中可能遇到的问题及相应的应对策略。最后，文章对标准偏差在大数据分析中的应用前景进行了展望，强调了标准偏差在数据分析领域的重要性以及未来发展方向。学习如何计算标准偏差，掌握标准差计算步骤与标准偏差公式，能够帮助我们更好地理解数据，提升数据分析能力。

理解标准偏差：数据的离散程度

标准偏差，也称标准差，是衡量数据离散程度的重要指标。它反映数据点偏离平均值的程度。数值越大，表示数据越分散；数值越小，表示数据越集中。

计算标准偏差，首先需要计算平均值（均值）。平均值是指所有数据之和除以数据个数。例如，有一组数据：2、4、4、4、5、5、7、9，其平均值为 (2+4+4+4+5+5+7+9)/8 = 5。

接着，计算每个数据点与平均值的差的平方。例如，对于数据点2，其与平均值的差为 2-5=-3，平方后为9。依次计算所有数据点的差的平方，并求和。

然后，将差的平方和除以数据个数减1（这是样本标准差的计算方法，如果是总体标准差，则除以数据个数）。结果即为方差。最后，将方差开平方根，得到标准差。

例如，上述数据组的方差为：[(2-5)²+(4-5)²+(4-5)²+(4-5)²+(5-5)²+(5-5)²+(7-5)²+(9-5)²]/(8-1) ≈ 4.67。标准差为√4.67 ≈ 2.16。这意味着这组数据点平均偏离均值约2.16个单位。

理解标准偏差有助于我们分析数据的分布情况，例如，在金融领域，股票的标准差可以反映其风险大小；在质量控制中，产品的标准差可以反映其质量的一致性。

不同场景下标准偏差的计算方法

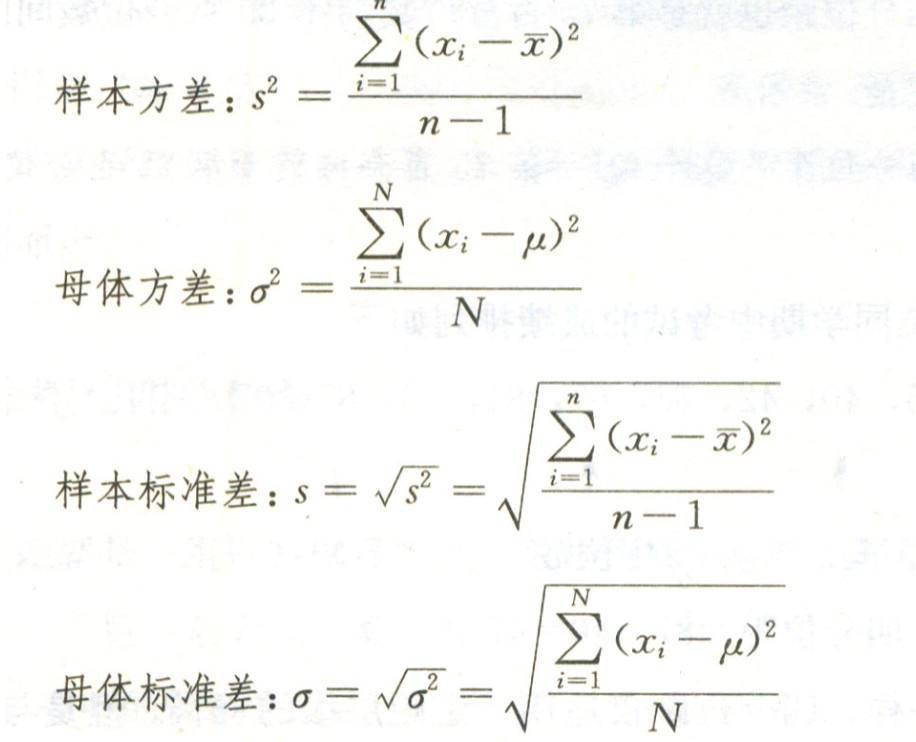
标准偏差的计算方法会根据数据的性质和用途有所不同。主要分为样本标准差和总体标准差两种。

样本标准差用于对样本数据的离散程度进行估计，其计算公式中分母为n-1（n为样本个数）。这是因为样本标准差需要对总体标准差进行无偏估计，使用n-1作为分母可以减小估计偏差，得到更准确的结果。例如，对某公司100名员工的薪资进行抽样调查，计算得到的标准差即为样本标准差。

总体标准差用于描述总体数据的离散程度，其计算公式中分母为n（n为总体个数）。只有当我们拥有全部总体数据时才能计算总体标准差。例如，对全国所有大学生的身高进行统计，计算得到的标准差即为总体标准差。

此外，对于分组数据，标准偏差的计算方法也略有不同，需要先计算每个组的平均值和频数，再根据公式进行计算。这在实际应用中比较常见，例如统计某个地区居民收入的标准差。

在实际应用中，选择合适的计算方法至关重要。错误的选择会导致数据分析结果的偏差，从而影响决策的准确性。

标准偏差的优缺点及应用场景

标准偏差作为一种常用的统计指标，具有其独特的优缺点。

优点：标准偏差能够有效地反映数据的离散程度，直观地展现数据分布的集中性和分散性。它不受数据量纲的影响，可以用于比较不同单位的数据。同时，标准偏差在统计推断中扮演着重要角色，例如假设检验和置信区间估计。许多统计模型和方法都依赖于标准偏差，例如正态分布和回归分析。

缺点：标准偏差容易受到极值的影响，当数据中存在极端值时，标准偏差会变得很大，无法真实反映数据的集中趋势。此外，标准偏差只能反映数据围绕平均值的离散程度，无法反映数据的形状和分布模式。一些非对称分布的数据，用标准差衡量离散程度可能存在误导。在实际应用中，需要结合其他统计指标，例如中位数、四分位数范围等，进行综合分析。

应用场景：标准偏差被广泛应用于各种领域，包括金融、工程、医学、社会科学等。在金融领域，标准偏差常用于衡量投资风险；在工程领域，标准偏差常用于质量控制和工艺改进；在医学领域，标准偏差常用于评估临床试验结果；在社会科学领域，标准偏差常用于分析社会现象和人口统计数据。

标准偏差计算中的误区及应对策略

• 错误地使用总体标准差和样本标准差：在样本数据的情况下，使用总体标准差公式会低估数据的离散程度。
• 忽略数据的分布形态：标准偏差只反映数据的离散程度，无法反映数据的形状和分布模式，对于非对称分布的数据，需要结合其他指标进行分析。
• 过度依赖标准偏差：标准偏差只是衡量数据离散程度的众多指标之一，不应将其作为唯一的判断依据。
• 对极值数据处理不当：极值数据会严重影响标准偏差的结果，需要进行相应的处理，如剔除异常值或采用稳健性统计方法。
• 忽视数据单位的影响：标准偏差的结果会受到数据单位的影响，在比较不同单位的数据时，需要进行标准化处理。

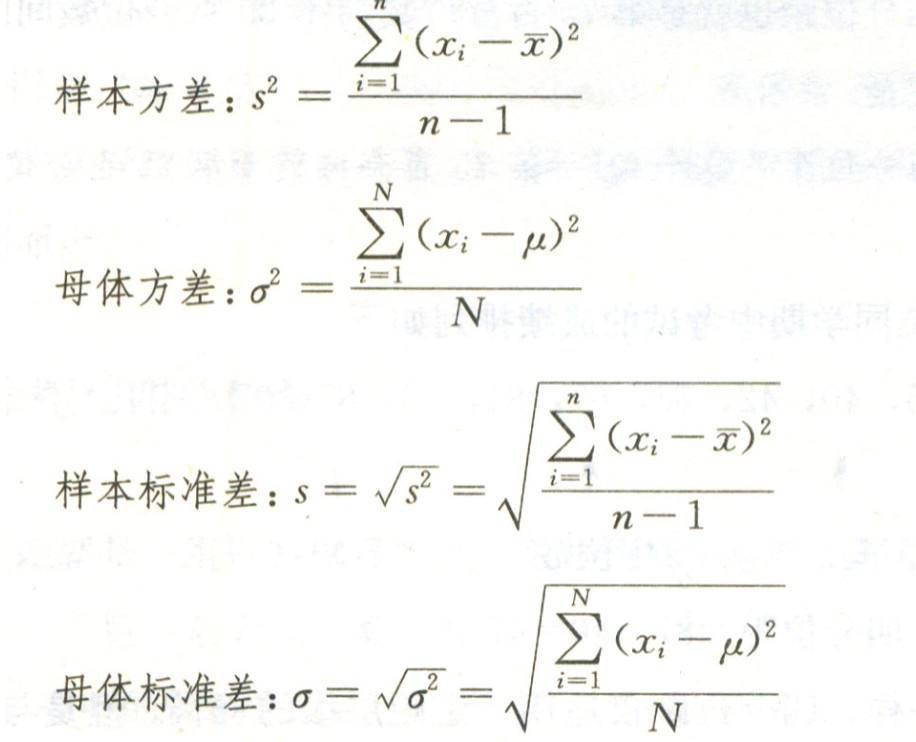
未来展望：标准偏差与大数据分析

随着大数据时代的到来，数据分析技术日新月异，标准偏差作为一种基础统计指标，也在不断发展和完善。在大数据分析中，标准偏差依然扮演着重要的角色，但其应用也面临着新的挑战。

首先，大数据的高维性和复杂性对标准偏差的计算和解释提出了更高的要求。传统的标准偏差计算方法可能难以处理海量数据，需要发展更高效的算法和工具。

其次，大数据的异质性和不确定性也增加了标准偏差的计算难度。如何处理缺失数据、异常值和噪声数据，是提高标准偏差计算准确性的关键。

最后，随着人工智能和机器学习技术的快速发展，标准偏差也可能被融入到更复杂的模型和算法中，用于解决更复杂的数据分析问题。例如，在风险管理领域，可以结合标准偏差和其他机器学习算法来构建更准确的风险预测模型。

未来，标准偏差的研究方向可能集中在提高计算效率、增强稳健性、以及与其他数据分析技术的集成上，以更好地适应大数据时代的数据分析需求。