几何平均数怎么算？详解计算方法及应用场景

本文深入浅出地讲解了几何平均数的计算方法、应用场景以及局限性。通过与算术平均数的对比，以及结合实际案例分析，读者可以清晰地理解几何平均数的优势和不足，并在实际应用中做出更明智的选择。文章还探讨了如何选择合适的平均数方法以及几何平均数在不同领域的应用，例如投资收益率计算、增长率分析等，最终目的是帮助读者掌握几何平均数的计算与应用，提升数据分析能力。

几何平均数的定义与基本计算方法

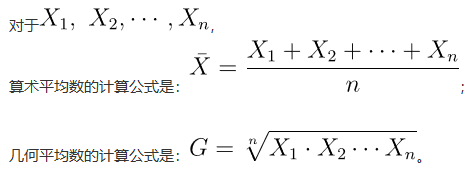
几何平均数，又称几何均数，是n个非负数的乘积的n次方根。它与算术平均数不同，更适用于计算比率、增长率等数据的平均值。

例如，一家公司连续三年的销售额增长率分别为10%、20%、30%，那么这三年的平均增长率该如何计算呢？如果直接使用算术平均数 (10%+20%+30%)/3 = 20%，则会高估实际平均增长率。此时，几何平均数就派上用场了。计算方法是：先将各年的增长率加1（即1.1、1.2、1.3），然后将它们相乘再开三次方，最后减去1，得到的结果即为几何平均增长率。

计算过程如下：(1.1×1.2×1.3)^(1/3) -1 ≈ 0.194 ≈ 19.4%。

可见，几何平均数更准确地反映了公司销售额的平均增长情况。

除了增长率，几何平均数也广泛应用于其他领域，例如计算投资组合的平均收益率等。在计算投资收益率时，几何平均数比算术平均数更能准确反映实际投资收益。这是因为几何平均数考虑了投资的复利效应，而算术平均数则忽略了复利效应。

几何平均数与算术平均数的比较与选择

几何平均数和算术平均数都是常用的平均数计算方法，但它们适用于不同的场景。算术平均数计算的是数据的简单平均值，适用于数据之间相互独立且没有关联的情况。而几何平均数计算的是数据的乘积的n次方根，更适用于计算比率、增长率、比例等数据，尤其是在计算投资收益率、人口增长率等数据时，几何平均数能更准确地反映数据的真实情况。

例如，计算某项投资连续几年的收益率时，如果使用算术平均数，将会高估实际的平均收益率，而几何平均数则能更准确地反映实际的平均收益率。这是因为算术平均数忽略了复利效应，而几何平均数考虑了复利效应。

在选择使用哪种平均数时，需要根据数据的具体情况进行判断。如果数据之间相互独立且没有关联，则可以使用算术平均数；如果数据之间存在关联，或者需要计算比率、增长率等数据，则应该使用几何平均数。

几何平均数的局限性及潜在风险

尽管几何平均数在许多情况下比算术平均数更准确，但它也存在一些局限性。首先，几何平均数的计算需要所有数据都为正数，如果数据中包含零或负数，则无法计算几何平均数。其次，几何平均数对极端值的敏感性较低，这在某些情况下可能会导致结果偏差。

例如，如果数据集中存在极端值（非常大或非常小），算术平均数会受到极端值的影响较大，而几何平均数则会相对稳定。但是，如果极端值代表了真实情况，那么几何平均数的稳定性反而可能掩盖了重要信息。

此外，在应用几何平均数时，还需要注意数据的可靠性和准确性。如果数据存在偏差或错误，则计算结果也会受到影响。因此，在使用几何平均数进行分析时，需要仔细审查数据的质量，并结合其他方法进行验证，以确保结果的可靠性。

几何平均数在不同领域的应用案例

几何平均数的应用非常广泛，在金融投资、经济增长、人口统计等领域都有着重要的应用。

例如，在金融投资中，几何平均数常用来计算投资组合的平均收益率。假设某投资组合在过去三年分别获得10%、20%、30%的收益率，那么这三年的平均收益率可以用几何平均数来计算，结果为19.4%。这比简单的算术平均数20%更准确地反映了投资的实际收益情况，因为几何平均数考虑了复利效应。

再比如，在人口统计中，几何平均数可以用来计算人口的平均增长率。如果某个地区在过去五年的人口增长率分别为5%、6%、7%、8%、9%，那么这五年的平均人口增长率可以用几何平均数来计算。

此外，在房地产评估中，也经常用到几何平均数，用于计算不同地段的房价平均增长率，来预测未来的房地产市场走势。总而言之，几何平均数是重要的统计工具，在多个领域中发挥着重要的作用。