梯形的上底和下底怎么区分？详解梯形几何特性及应用

本文深入浅出地讲解了梯形上底和下底的区分方法，从定义、几何特性、实际应用等多个角度进行了分析，并结合实际案例进行了说明。文中详细解释了如何根据梯形的平行边长度来区分上底和下底，以及在实际应用中如何运用这一知识。读者可以通过本文掌握梯形上底和下底的区分方法，并解决相关计算难题，提升对梯形几何知识的理解。

梯形上底和下底的定义与基本区分

理解梯形上底和下底的关键在于认识梯形的几何定义。梯形是只有一组对边平行的四边形。平行的那组对边分别称为梯形的两底，其中较长的那条边称为下底，较短的那条边称为上底。

这看起来很简单，但有时在实际应用中，特别是当梯形倾斜或不规则时，区分上底和下底可能会变得棘手。例如，在一个倾斜的梯形中，如果我们仅仅凭直观判断，可能会出现错误。这时候，我们需要借助一些辅助工具或者方法进行精确的判断，比如测量平行边的长度，或者通过坐标系进行计算。

为了更加清晰地理解，我们可以想象一个普通的梯子。梯子的两条长边平行且长度不等，其中靠地面的较长边类似于梯形的下底，而上方较短的边类似于梯形的上底。这个类比有助于我们更好地理解上底和下底的含义。

记住，无论梯形形状如何变化，上底和下底始终是那对平行的边，且上底总是短于下底。

不同角度观察梯形上底和下底

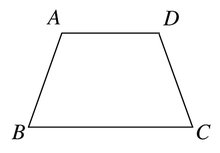
从不同的角度审视梯形上底和下底的区分，可以加深我们对这一几何概念的理解。首先，我们可以从几何学的角度来理解：梯形的上底和下底是其平行边的名称，长度不等。这个定义是区分上底和下底最根本、最可靠的方法。

其次，我们可以从计算的角度来看待：在计算梯形的面积时，上底和下底是必不可少的参数。不同的计算公式会用到上底和下底的长度。

再从实际应用的角度考虑，例如在土木工程中，我们会遇到各种形状的梯形结构，例如屋顶、斜坡等。工程师们需要精确地测量上底和下底的长度，才能计算出准确的面积和体积。

一些不规则梯形，可能会让我们难以直观区分上底和下底，这时可以通过测量平行边之间的距离来确定。距离较大的那条边，即为下底，而距离较小的那条边为上底。

总而言之，无论从理论还是实践层面，上底和下底的区分都是明确的，关键在于我们是否理解了梯形的本质属性。

梯形上底和下底在实际生活中的应用

• 建筑工程中的斜屋顶设计：许多房屋的屋顶设计成梯形，需要精确计算上底和下底长度来确定屋顶的面积和用料。
• 道路工程中的边坡稳定性分析：在进行边坡稳定性分析时，边坡常常被简化成梯形模型，上底和下底的确定直接影响分析结果的准确性。
• 水利工程中的渠道设计：梯形渠道广泛应用于水利工程中，需要准确测量上底和下底的长度来计算渠道的流量和排水能力。
• 农业中的梯田建设：梯田的形状通常是梯形，上底和下底的比例决定了梯田的面积和土壤的利用效率。
• 艺术设计中的几何图案：在艺术设计中，梯形作为一种几何图形，可以用来创造出具有独特视觉效果的图案，上底和下底的比例和位置影响着图案的美感。

总结：如何准确区分梯形上底和下底

总而言之，区分梯形上底和下底的关键在于理解其几何定义：只有一组对边平行的四边形，平行且长度不等的两条边就是梯形的上下底，其中较长的一条是下底，较短的一条是上底。

在实际应用中，我们可能会遇到各种复杂的梯形，这时需要结合具体情况，采用测量、计算等多种方法进行准确区分。无论是从几何定义、计算公式还是实际应用角度出发，只要牢记上底小于下底这个基本原则，就能准确区分梯形的上底和下底。

对于初学者来说，多练习，多观察不同形状的梯形，就能逐渐掌握区分上底和下底的方法。掌握这一基础几何概念，对于学习更高级的几何知识至关重要。