正方体的体积怎么求？公式、计算方法及应用详解

本文详细阐述了正方体的体积计算方法，从公式推导、实际应用到误区分析，并探讨了其在高等数学中的拓展。文中结合生活实例，深入浅出地讲解了“正方体的体积怎么求”，以及长方体体积计算方法等相关长尾关键词，希望能帮助读者更好地理解和运用正方体体积计算知识。

正方体体积公式及推导

正方体的体积计算是几何学中的基本问题，其公式简单易懂，但理解其背后的推导过程能更好地掌握其本质。

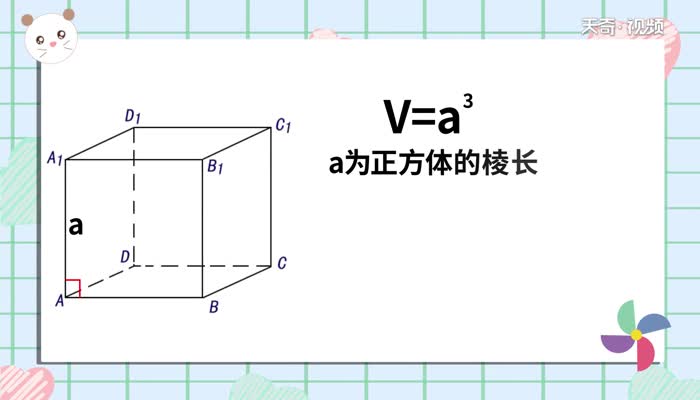
正方体的体积计算公式为：V = a³，其中 V 代表体积，a 代表正方体的棱长。

这个公式的推导可以从其几何特性出发：正方体是由六个完全相同的正方形面围成的立体图形。我们可以想象将正方体分解成许多个边长为1的小正方体，棱长为a的正方体就可以分解成a*a*a个这样的单位小正方体。因此，正方体的体积就等于a*a*a = a³。

理解这个推导过程，可以帮助我们更好地理解体积的概念，以及正方体这种特殊几何形状的体积计算方式。例如，一个棱长为5厘米的正方体，其体积为5³=125立方厘米。这不仅仅是一个简单的公式，更体现了数学中的归纳与演绎推理。从简单的单位小正方体出发，通过累加最终得出正方体的体积公式。

实际应用中，我们常常会遇到一些非整数的棱长，这时仍可以用该公式计算，例如棱长为2.5厘米的正方体，体积为2.5³=15.625立方厘米。

正方体体积计算在生活中的应用

正方体的体积计算并非仅仅是数学课本中的一个抽象概念，它在日常生活中有着广泛的应用。

例如，在建筑工程中，计算房屋地基的体积、水泥预制板的体积都需要用到正方体的体积计算公式。如果需要计算一个正方体形状的水泥池的容积，只需要测量其棱长，然后代入公式V=a³即可快速计算出其容积，这对于工程进度安排和材料预算至关重要。

在包装行业中，正方体形状的包装盒非常常见。计算包装盒的体积可以帮助我们确定包装材料的用量，并优化包装设计，降低成本。例如，一个电子产品包装盒，如果其形状是正方体，我们可以通过计算其体积来评估包装盒的成本以及运输效率。

此外，在日常生活中，我们也常常会遇到一些与正方体相关的体积计算问题，例如计算一个正方体形状的储物盒的容积等等。掌握正方体体积的计算方法，可以帮助我们更好地解决这些实际问题。

正方体体积计算的误区及注意事项

• 单位换算错误：在进行计算前，务必确保所有单位一致，例如厘米、米等。如果单位不一致，会导致计算结果错误。
• 公式应用错误：一些同学会误将正方体的表面积公式与体积公式混淆，导致计算错误。记住正方体体积公式为V=a³。
• 棱长测量不准确：棱长是正方体体积计算的关键，如果棱长测量不准确，会导致计算结果的偏差。需要使用精确的测量工具进行测量。
• 忽略实际情况：在实际应用中，正方体可能并非完全规则，例如存在一些微小的缺损或变形。这时需要根据实际情况进行适当的调整，并考虑误差的影响。
• 计算结果单位错误：计算结果应带上正确的单位，例如立方厘米或立方米，并根据实际情况选择合适的单位。

正方体体积计算的拓展与延伸

正方体体积的计算是学习立体几何的基础，它可以帮助我们理解更复杂的几何体的体积计算方法。

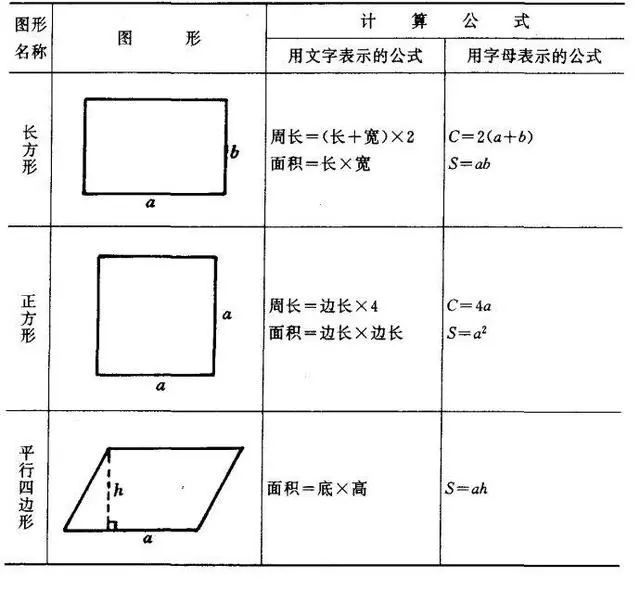
例如，长方体的体积计算公式V=abc (a, b, c分别为长方体的长宽高)，就可以看作是正方体体积公式的推广。理解了正方体体积的计算方法，我们就可以更容易地理解长方体、立方体等其他立体图形的体积计算方法。

此外，正方体体积计算也与积分、微积分等高等数学概念密切相关。在高等数学中，我们会学习到如何利用积分的方法来计算各种不规则形状的体积，而正方体体积的计算则为理解这些更高级的计算方法提供了基础。

因此，掌握正方体体积的计算方法，不仅可以解决日常生活中的一些实际问题，还可以为我们进一步学习高等数学打下坚实的基础。 这对于未来学习更高级的数学知识至关重要，例如，理解空间几何的概念、以及在物理学、工程学等其他学科中的应用。