梯形的面积怎么求？公式推导、应用及常见问题详解

本文详细讲解了梯形的面积怎么求，从公式推导、不同类型梯形的计算方法、实际应用案例以及常见问题解决方法等多个角度进行了深入分析。文章强调了理解梯形高和单位换算的重要性，并通过实际案例说明了梯形面积计算在工程和农业等领域的广泛应用，旨在帮助读者掌握梯形面积计算技巧，解决实际问题。

梯形面积公式的推导与理解

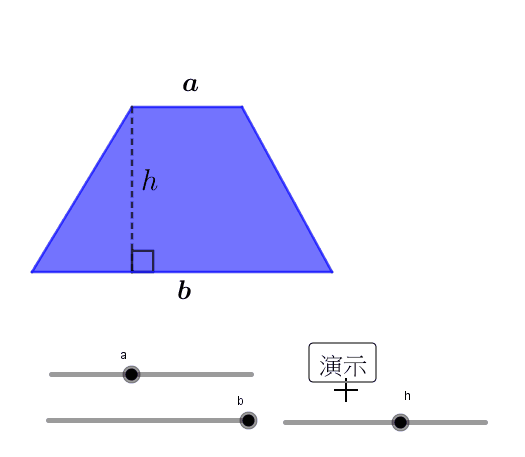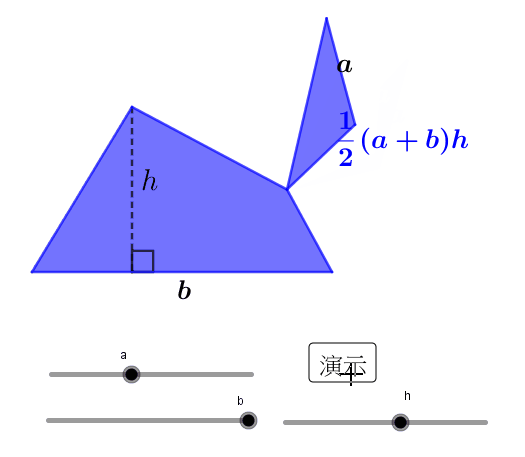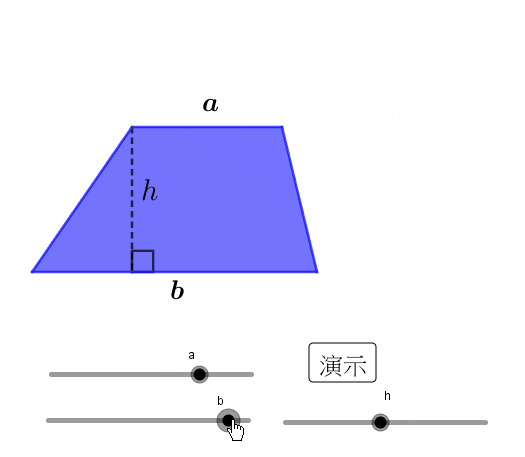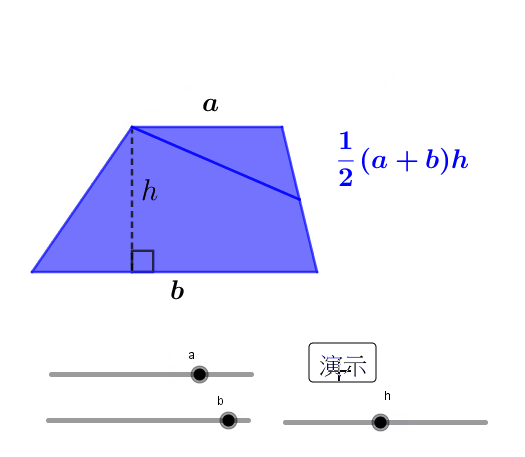
梯形的面积计算是平面几何中的基础知识，也是许多实际问题中的关键步骤。我们通常使用的梯形面积公式是：S = (a+b)h/2，其中，a 和 b 分别代表梯形的上下底长度，h 代表梯形的高。

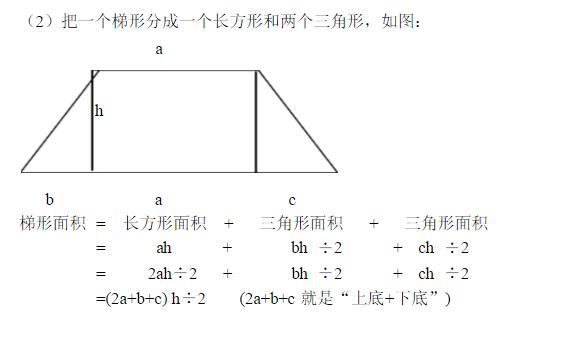
这个公式的推导过程可以借助于将梯形转化为平行四边形来理解。我们可以将一个梯形复制一份，将其上下底对接，然后旋转180度，与原梯形组合成一个平行四边形。这个平行四边形的底长是a+b，高是h，面积是(a+b)h。而原梯形的面积只是这个平行四边形面积的一半，因此梯形的面积公式就推导出来了。

理解这个公式的关键在于理解梯形的高的概念。梯形的高指的是两底之间垂直距离的最短距离。在实际应用中，我们需要注意区分梯形的高和梯形的斜边。有些题目中可能会给出梯形的斜边长度，而不是高，这时需要运用三角函数或勾股定理来求出梯形的高，再代入公式计算面积。例如，一个等腰梯形，已知上底、下底和腰长，我们可以通过作高，将梯形分成矩形和两个直角三角形，利用勾股定理求出高。

掌握梯形面积公式，对于解决各种与面积相关的几何问题至关重要。例如，在土木工程中，计算梯形土地面积；在室内设计中，计算梯形房间的面积等等，都需要用到这个公式。

不同类型梯形的面积计算

除了常见的梯形，还有一些特殊的梯形，例如等腰梯形、直角梯形等。这些梯形的面积计算方法与普通梯形类似，只是在求高或底的过程中可能需要用到一些特殊的技巧。

例如，对于等腰梯形，我们可以通过作高，将等腰梯形分成一个矩形和两个全等的直角三角形。如果已知上底、下底和腰长，则可以利用勾股定理求出高。对于直角梯形，其中一条腰是高，计算面积时直接使用公式即可。

在实际应用中，我们可能会遇到一些不规则的梯形，这时我们可以将不规则梯形分解成若干个规则图形（如三角形、矩形）的组合，分别计算这些规则图形的面积，然后将它们的面积加起来，得到不规则梯形的总面积。例如，一个复杂的梯形可以分割成一个矩形和两个三角形，分别计算面积后再求和。这需要一定的几何分析能力和空间想象能力。

熟练掌握不同类型梯形的面积计算方法，能够更好地应对各种实际问题。例如，在测量土地面积时，如果土地形状为梯形，则需要根据梯形的类型选择合适的计算方法。

梯形面积计算的实际应用与案例分析

梯形面积计算在实际生活中有着广泛的应用，例如在建筑工程中计算房屋的面积，在农业中计算田地的面积，在工业中计算零件的面积等等。

例如，一个建筑工地需要计算一个梯形形状的地基的面积，以便估算工程量和材料用量。工程师会根据实地测量结果，得到地基的上底、下底和高，然后利用梯形面积公式计算出地基的面积。如果地基形状不规则，则需要先将不规则图形分割成若干个梯形，再分别计算每个梯形的面积，最后求和。

另一个例子是，在农业生产中，需要计算梯形形状的田地的面积，以便确定施肥量和灌溉量。农民会根据田地的实际情况，测量田地上底、下底和高，然后利用梯形面积公式计算出田地的面积。这对于精确的农业管理至关重要。

通过以上案例，我们可以看到梯形面积计算在实际应用中的重要性，掌握这项技能对于解决实际问题至关重要。

梯形面积计算中可能遇到的问题及解决方法

• 单位换算问题：在计算梯形面积时，需要注意单位的一致性。例如，如果上底和下底的单位是米，而高的单位是厘米，则需要先将单位换算成一致的单位，再进行计算。
• 数据测量误差：在实际测量中，不可避免地会存在一些测量误差。这些误差会影响梯形面积的计算结果。为了减少误差的影响，需要采用精确的测量工具，并进行多次测量取平均值。
• 图形复杂性：有些梯形形状比较复杂，难以直接运用公式计算。这时需要先将复杂的梯形分解成若干个简单的梯形或其他几何图形，分别计算它们的面积，再求和。
• 高程的确定：在一些地形测量中，需要计算梯形地块的面积，这其中高程的确定至关重要，应考虑地形起伏的影响。
• 公式选择错误：在选择公式时，应根据梯形的具体类型选择合适的公式，避免因为公式选择错误导致计算结果出现偏差。