梯形的上底怎么求？详解梯形上底计算方法及应用场景

本文系统地讲解了如何求梯形的上底，涵盖了已知不同条件下的计算方法，并分析了不同类型梯形的特殊解法以及常见错误和避免方法。 掌握这些技巧，能够轻松应对各种梯形上底的计算问题，特别是在已知梯形面积、下底和高，以及已知梯形周长、下底和两腰长等常见情况下。

已知梯形面积、下底和高，如何求上底？

求梯形上底最常见的情况是已知梯形的面积、下底和高。梯形的面积公式为：S = (a+b)h/2，其中S为面积，a为上底，b为下底，h为高。

如果我们已知S、b和h，则可以将公式变形为：a = 2S/h - b。

例如，一个梯形的面积为30平方厘米，下底为8厘米，高为5厘米，则上底a = (2*30)/5 - 8 = 12 - 8 = 4厘米。

这个方法简单易懂，是求梯形上底最基础、最常用的方法。需要注意的是，公式的适用条件是梯形必须是平面图形，且高必须垂直于上下底。如果高不是垂直的，则需要先将其分解成直角三角形和矩形再进行计算。

根据这个公式进行计算时，需要特别注意单位的统一，避免出现计算错误。在实际运用中，如果遇到较为复杂的梯形，可尝试将其分解成多个简单图形求解，从而更容易求得最终结果。

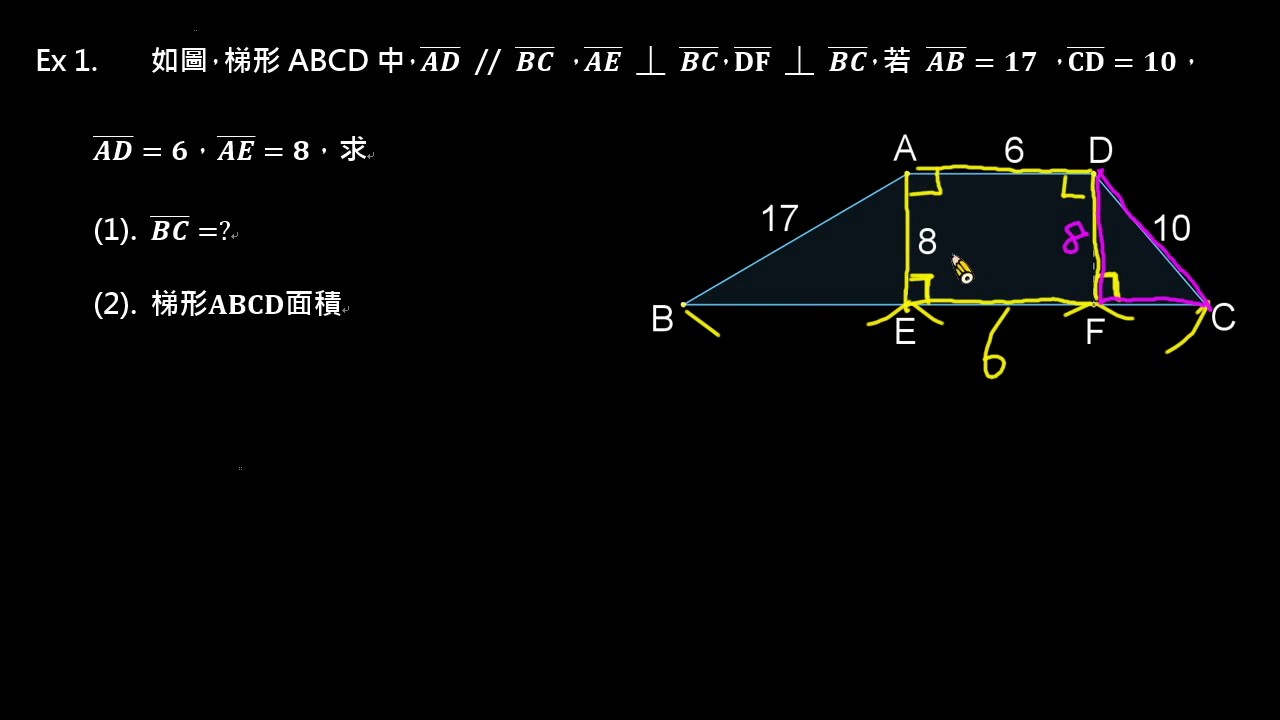
已知梯形周长、下底、两腰长，如何求上底？

当已知梯形的周长、下底和两腰长时，求上底需要借助勾股定理或其他几何关系。由于梯形本身形状的不确定性，单纯依靠周长、下底和两腰长并不能直接计算出上底的长度。我们需要结合其他条件或信息，例如梯形的类型(等腰梯形、直角梯形等)。

对于等腰梯形，我们可以利用其对称性，通过构造辅助线将梯形分解成多个更容易计算的图形。

例如，假设一个等腰梯形的周长为20厘米，下底为8厘米，两腰长均为5厘米。我们可以画一条高，将梯形分成一个矩形和两个直角三角形。根据勾股定理，我们可以算出高，然后就可以根据梯形面积公式来求出上底。

对于非等腰梯形，则需要更多条件才能确定其上底长度，例如可以知道一个腰长和与该腰长对应的底角。需要注意的是，在运用勾股定理时，要注意直角三角形的判断以及勾股定理的应用，确保计算结果的准确性。

不同类型梯形的特殊解法

不同类型的梯形，求上底的方法也会有所不同。例如，对于直角梯形，可以利用其直角的特性，运用勾股定理或三角函数来求解。对于等腰梯形，可以利用其对称性，通过构造辅助线简化计算过程。

在处理实际问题时，要根据题目的具体条件选择合适的方法，切忌生搬硬套。 一个典型的例子是测量土地面积。如果土地的形状是一个梯形，而我们只知道梯形的下底、高和面积，那么就可以利用上述公式直接计算出上底的长度，从而计算出土地的具体面积。

此外，在工程设计和建筑领域，也经常会遇到梯形结构。例如，在计算桥梁的受力情况时，需要计算梯形梁的截面面积，而这又需要知道梯形的上底。通过精确计算上底的长度，才能确保结构设计的安全可靠。

对于一些特殊的梯形，例如其上底为0的退化情况，此时它实际上就是一个三角形，其计算方法就要改变。 需要根据具体题目仔细分析已知条件。

梯形上底计算中的常见错误及避免方法

在计算梯形上底的过程中，一些常见的错误包括：单位不统一、公式使用错误、数据输入错误以及忽略特殊情况（如退化成三角形）。

为了避免这些错误，我们需要认真检查题目中的已知条件，确保单位统一（例如都使用厘米或米），选择正确的公式，并仔细核对数据的准确性。

另外，在计算过程中，最好能够进行步骤拆解，逐步计算，方便发现和纠正错误。 良好的计算习惯和仔细认真的态度，是避免错误的关键。例如，在计算过程中，可以先将公式写出来，再代入数值，并检查每一步骤的计算结果，尽量避免计算错误。

还可以运用不同的方法进行交叉验证。比如在已知条件允许的情况下，可以使用不同的方法来求上底，如果得到的结果一致，那么可以大大提高计算结果的可靠性。这对于一些复杂的几何问题尤其重要。