矩阵相乘怎么算？深入剖析矩阵乘法运算及应用

本文深入探讨了矩阵相乘的计算方法、应用场景、优缺点以及未来发展趋势。从基本概念到高级应用，详细阐述了矩阵乘法在不同领域的应用，并分析了其在实际应用中面临的挑战。文章还介绍了多种矩阵乘法类型及其应用，例如稀疏矩阵乘法、块矩阵乘法等。通过学习本文，读者可以全面掌握矩阵相乘的计算方法，并理解其在实际应用中的重要意义。

矩阵乘法的基本概念和计算步骤

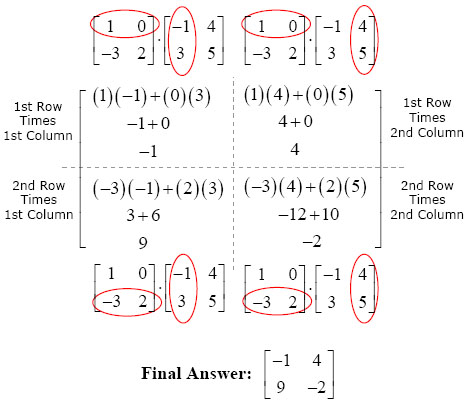
矩阵相乘是线性代数中的一个重要运算，它在计算机图形学、机器学习等领域有着广泛的应用。那么，矩阵相乘怎么算呢？首先，我们需要明确矩阵乘法的定义：只有当第一个矩阵的列数等于第二个矩阵的行数时，两个矩阵才能相乘。

假设我们有两个矩阵 A 和 B，A 是一个 m × n 的矩阵，B 是一个 n × p 的矩阵，那么它们的乘积 C 将是一个 m × p 的矩阵。矩阵 C 中的每个元素 Cij 是由 A 矩阵的第 i 行和 B 矩阵的第 j 列对应元素相乘再求和得到的。

例如，假设 A = [[1, 2], [3, 4]]，B = [[5, 6], [7, 8]]。那么 A × B 的计算过程如下：

C11 = (1 × 5) + (2 × 7) = 19

C12 = (1 × 6) + (2 × 8) = 22

C21 = (3 × 5) + (4 × 7) = 43

C22 = (3 × 6) + (4 × 8) = 50

因此，A × B = [[19, 22], [43, 50]]。理解这个基本计算步骤是掌握矩阵相乘的关键。

矩阵乘法不满足交换律，即 A × B ≠ B × A，这与普通的数乘不同，需要特别注意。 这在实际应用中，例如在计算机图形变换中，矩阵的顺序决定了变换的先后顺序，从而影响最终结果。

不同类型的矩阵乘法及其应用场景

除了基本矩阵乘法，还有其他类型的矩阵乘法，例如：稀疏矩阵乘法、块矩阵乘法等等。

稀疏矩阵是指矩阵中大部分元素为零的矩阵。对于稀疏矩阵，直接采用标准的矩阵乘法算法效率较低，因为大量的计算都是0与其他数字的乘法。因此，针对稀疏矩阵，会采用一些特殊的算法，例如只计算非零元素之间的乘法，以提高运算效率。

块矩阵乘法则是将矩阵划分成若干个子块，然后对子块进行矩阵乘法运算。这种方法在并行计算中应用广泛，因为它可以将矩阵乘法运算分解成多个独立的任务，从而提高计算速度。在大型的科学计算中，比如天气预报的数值模拟，经常用到块矩阵的乘法来提升运算速度。

此外，在实际应用中，还会根据具体问题的特点选择合适的矩阵乘法算法。例如，在图像处理中，为了提高图像处理的效率，会使用快速傅里叶变换等算法来进行矩阵乘法运算。

矩阵相乘的优缺点分析：效率与复杂性

矩阵相乘虽然在很多领域发挥着重要作用，但也存在一些局限性。

优点：矩阵乘法是一种高效的计算工具，它可以将多个线性变换组合成一个矩阵，从而简化计算过程。在处理大量数据时，矩阵运算的效率远高于逐个元素的计算。例如在图像处理中，一个图像可以表示为一个矩阵，图像的旋转、缩放等操作都可以通过矩阵乘法来实现，这使得图像处理的速度大幅提升。

缺点：矩阵相乘的计算复杂度相对较高。对于一个 n × n 的矩阵，其乘法运算的时间复杂度为 O(n³)，当 n 很大时，计算时间会急剧增加。这就导致在处理超大规模矩阵时，计算时间可能非常长。

为了提高计算效率，研究人员不断开发新的矩阵乘法算法，例如 Strassen 算法等，这些算法能够降低计算复杂度，提高计算速度。

矩阵乘法在实际应用中的挑战与未来发展趋势

• 随着大数据时代的到来，矩阵运算的规模越来越大，对计算资源的需求也越来越高。如何设计更高效的矩阵乘法算法，是未来研究的一个重要方向。
• 在量子计算领域，研究人员正在探索利用量子计算的优势来加速矩阵乘法运算。
• 此外，如何将矩阵乘法与其他算法结合起来，提高算法的整体效率，也是一个值得研究的问题。
• 深度学习和人工智能技术的快速发展也对矩阵乘法提出了新的要求。如何设计出适合深度学习模型的矩阵乘法算法，是一个重要的研究方向。
• 在分布式计算环境下，如何高效地进行矩阵乘法运算也是一个挑战。