矩阵的迹怎么求？详解矩阵迹的计算方法及应用场景

本文深入探讨了矩阵的迹怎么求，从定义、计算方法、性质到实际应用和未来发展趋势进行了全面的阐述。文章详细介绍了矩阵迹在不同领域的应用，并指出了大型矩阵迹计算的挑战和未来发展方向，例如Python矩阵迹计算、机器学习中的矩阵迹等长尾关键词的应用。

矩阵迹的定义与基本计算方法

矩阵的迹，简单来说，就是矩阵主对角线元素之和。对于一个 n×n 的方阵 A，其迹记作 tr(A) 或 Tr(A)，计算方法是将 A 的所有主对角线上的元素加起来。例如，一个 2×2 的矩阵 A = [[a, b], [c, d]]，它的迹就是 tr(A) = a + d。

理解矩阵迹的定义是掌握其计算方法的关键。对于大型矩阵，直接相加固然可行，但效率不高。尤其在计算机编程中，使用循环进行计算更为高效和规范。例如，在 Python 的 NumPy 库中，可以使用 `numpy.trace()` 函数方便快捷地计算矩阵的迹。

此外，理解迹的定义有助于我们认识到迹的一些重要性质，比如迹的线性性：tr(A + B) = tr(A) + tr(B) 以及 tr(kA) = k tr(A)，其中 k 为常数。这些性质在后续的矩阵运算和证明中非常有用，例如在计算矩阵乘积的迹时，我们可以利用这些性质简化计算过程。许多线性代数的证明都依赖于迹的这些性质。

值得注意的是，迹只对方阵有定义。对于非方阵，迹的概念并不适用。这是因为非方阵的主对角线元素数量是不确定的，无法进行求和运算。

矩阵迹的性质及其在证明中的应用

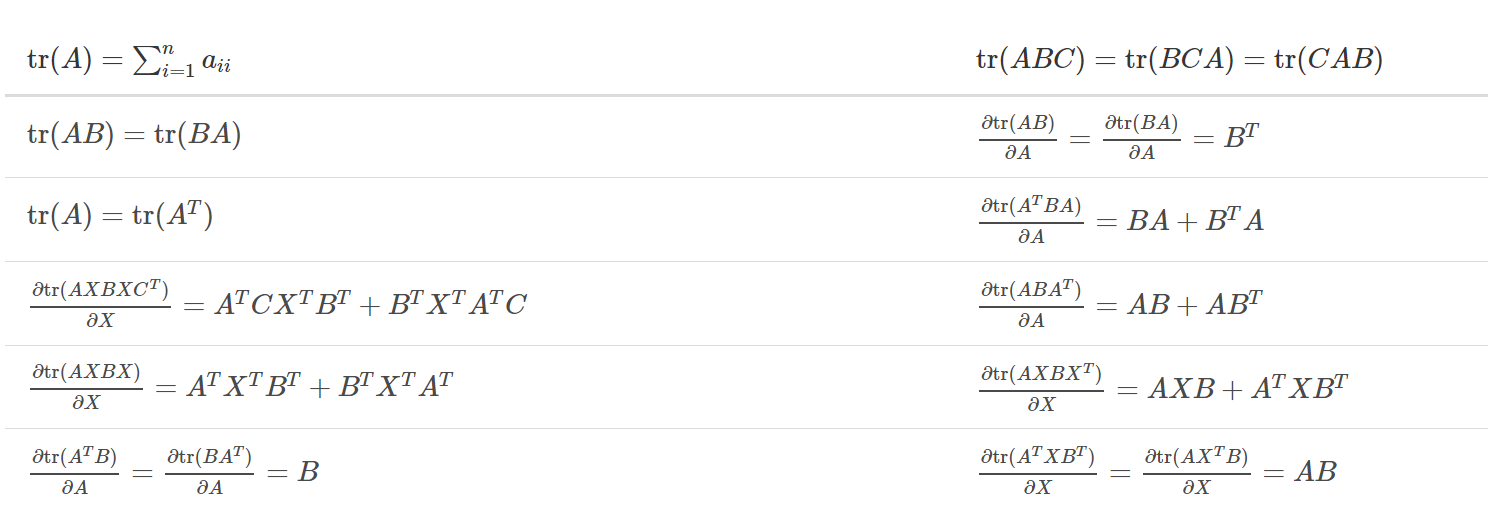
矩阵的迹拥有许多重要的性质，这些性质使得矩阵迹在数学证明和计算中发挥着重要作用。除了前面提到的线性性，还有迹的循环性质：对于两个可乘的矩阵 A 和 B，tr(AB) = tr(BA)。这一性质在许多线性代数证明中被广泛运用，例如证明相似矩阵的迹相等。

另一个重要的性质是迹的转置不变性：tr(A) = tr(Aᵀ)。这在处理矩阵转置问题时非常方便。例如，如果需要计算一个矩阵转置的迹，我们可以直接计算原矩阵的迹，从而简化计算。

这些性质并非孤立存在，它们之间相互关联，共同构成了矩阵迹的理论基础。充分理解这些性质，可以帮助我们更深入地理解矩阵的性质，并在实际应用中高效地进行计算和证明。例如，在证明矩阵相似性的过程中，利用迹的性质可以简化证明过程，从而提高证明效率。

不同编程语言中矩阵迹的计算

• 在 Python 中，可以使用 NumPy 库的 `numpy.trace()` 函数直接计算矩阵的迹。该函数效率高且易于使用。
• MATLAB 也有内置函数 `trace()` 可用于计算矩阵的迹，使用方法与 NumPy 类似。
• 在 C++ 中，可以使用 Eigen 库，Eigen 库提供了一个高效的矩阵运算库，其中包含了计算矩阵迹的函数。
• Java 中可以使用一些线性代数库，例如 Apache Commons Math，来计算矩阵的迹。
• R 语言中也提供了计算矩阵迹的函数，方便用户进行相关计算。

矩阵迹在实际应用中的案例分析

矩阵的迹并非仅仅是线性代数中的一个抽象概念，它在许多实际应用中都有着重要的作用。在机器学习领域，矩阵的迹经常用于计算方差、协方差等统计量，例如在主成分分析（PCA）中，需要计算协方差矩阵的迹来衡量数据的方差。

在图像处理中，矩阵迹也可以用来描述图像的某些特征。例如，图像的灰度矩阵的迹可以用来衡量图像的整体亮度。

在物理学中，矩阵迹也有着广泛的应用，例如在量子力学中，量子态的密度矩阵的迹表示系统的归一化条件。这些应用体现了矩阵迹作为一种重要的数学工具在不同领域的实用价值。深入学习矩阵迹，有助于我们更好地理解这些领域的理论和方法。

此外，在工程控制领域，矩阵迹也经常用于系统分析和设计中。例如，在求解线性系统的稳定性问题中，可以使用矩阵迹来判断系统矩阵的特征值是否都在左半平面，从而判断系统的稳定性。

矩阵迹计算的潜在挑战与未来发展趋势

尽管计算矩阵的迹相对简单，但在处理超大型矩阵时，仍然会面临计算效率和内存限制的挑战。随着大数据时代的到来，需要处理的矩阵规模越来越大，这对于矩阵迹的计算提出了更高的要求。因此，发展更高效的算法和并行计算技术至关重要。

未来，矩阵迹的计算可能会与人工智能技术相结合，例如利用深度学习算法来优化矩阵迹的计算过程，或者利用GPU加速计算。此外，在量子计算领域，探索利用量子计算机来计算矩阵迹也可能成为未来的发展方向。

同时，随着对矩阵理论研究的深入，可能会发现矩阵迹更多新的性质和应用，进而拓展其在不同领域的应用范围。这需要数学家和计算机科学家持续的努力和探索。