三个数的最小公倍数怎么求？详解求解方法及应用场景

本文深入浅出地讲解了如何求三个数的最小公倍数，涵盖了分解质因数法、短除法等常用方法，并结合实际案例分析了最小公倍数在生活、工程等领域的应用，同时也探讨了该方法的未来发展趋势。掌握这些技巧，能轻松解决各种与最小公倍数相关的难题，例如如何计算三个周期性事件的重合时间等。

理解最小公倍数的概念

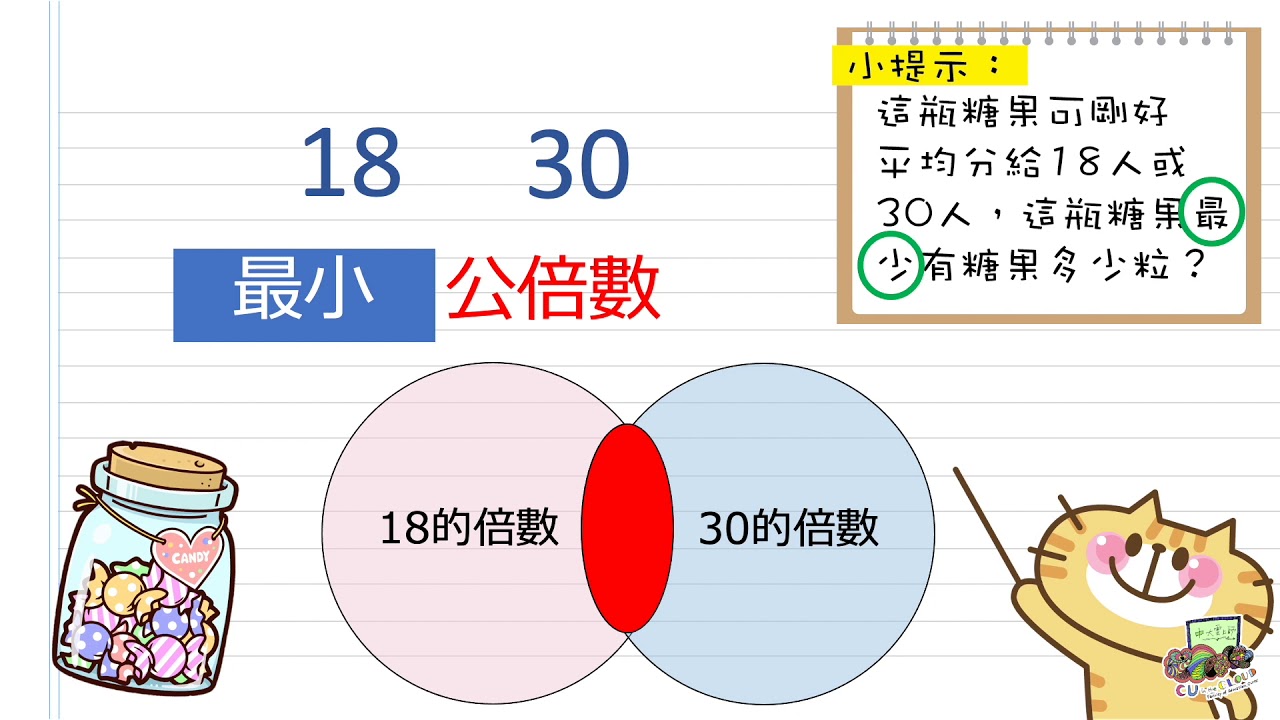
在学习如何求三个数的最小公倍数之前，我们需要先理解最小公倍数的概念。最小公倍数（Least Common Multiple，LCM）是指几个整数的公倍数中最小的那一个。例如，6和8的公倍数有24, 48, 72等等，其中最小的就是24，所以6和8的最小公倍数是24。

理解最小公倍数的概念对于掌握后续的求解方法至关重要。许多实际问题，例如安排工作计划、计算周期性事件的重合时间等，都需要运用最小公倍数的知识。例如，如果甲每3天值班一次，乙每4天值班一次，丙每6天值班一次，那么他们三人同时值班的周期是多少天？这就需要求出3、4、6的最小公倍数。

求解最小公倍数的方法有很多种，不同的方法适用于不同的情况，在选择方法时，需要根据具体数字的特点来决定。

三个数最小公倍数的常用求解方法

求三个数的最小公倍数，最常用的方法是分解质因数法。这种方法的步骤是：首先将每个数分解成质因数的乘积形式；然后找出所有质因数中指数最大的那些；最后将这些质因数相乘，得到的积就是这三个数的最小公倍数。

例如，求6、15和20的最小公倍数。先将它们分解质因数：6 = 2 × 3；15 = 3 × 5；20 = 2² × 5。然后找出所有质因数中指数最大的：2²、3、5。最后相乘：2² × 3 × 5 = 60。所以6、15和20的最小公倍数是60。

除了分解质因数法，还可以使用短除法求最小公倍数。短除法是一种更为直观的计算方法，特别适合于数字较小的场合。先用这三个数的最小质数去除，直到三个数变成互质数。然后将所有除数的乘积相乘，便是这三个数的最小公倍数。

最小公倍数的应用及实际案例分析

• 在日常生活中，最小公倍数的应用十分广泛，例如安排工作计划、计算周期性事件的重合时间等。
• 在工程项目中，最小公倍数可以用来确定最短的施工周期或设备维护周期。
• 在音乐理论中，最小公倍数可以用来计算不同音符的节拍关系。
• 在计算机科学中，最小公倍数可以用来优化算法，例如寻找公约数。
• 在化学中，最小公倍数可以用来计算化学反应的配平系数。

求解三个数最小公倍数的技巧和注意事项

在实际应用中，求解三个数的最小公倍数时，需要注意一些技巧和注意事项，以提高计算效率和准确性。首先，要仔细观察这三个数的特点。如果其中有几个数有公约数，则可以先约分，再求最小公倍数，可以简化计算。

其次，要选择合适的方法。如果数字比较小，可以使用短除法；如果数字比较大，或包含较多质因子，则使用分解质因数法更为高效。

再次，在计算过程中，要认真细致，避免出现错误。最后，可以运用计算器或计算机软件进行辅助计算，提高效率。例如，一些计算器或软件中内置了最小公倍数的计算功能，可以方便快捷地求出结果。

最小公倍数求解方法的未来发展趋势

随着计算机技术的发展，求解最小公倍数的方法也在不断改进。未来，基于人工智能和机器学习的算法可能会进一步优化最小公倍数的计算过程，提高计算速度和效率。

同时，新的算法也可能会被开发出来，以适应更复杂、更高维度的计算需求。例如，在处理大型数据集时，传统的算法可能会显得效率低下，因此需要开发更加高效的算法。此外，未来研究或许会探索最小公倍数在更多领域的应用，以及其与其他数学概念的结合。