正方形的面积怎么求？公式推导、应用案例及常见问题解答

本文详细阐述了正方形面积计算公式S=a²的推导过程及其实际应用，并分析了计算过程中常见的误区，例如单位换算错误和测量精度不足。此外，文章还展望了未来正方形面积计算方法的发展趋势，例如人工智能和自动化技术应用带来的效率提升。通过学习本文，读者可以更加熟练地掌握正方形面积的计算方法，并在实际生活中灵活运用。

正方形面积公式的推导与理解

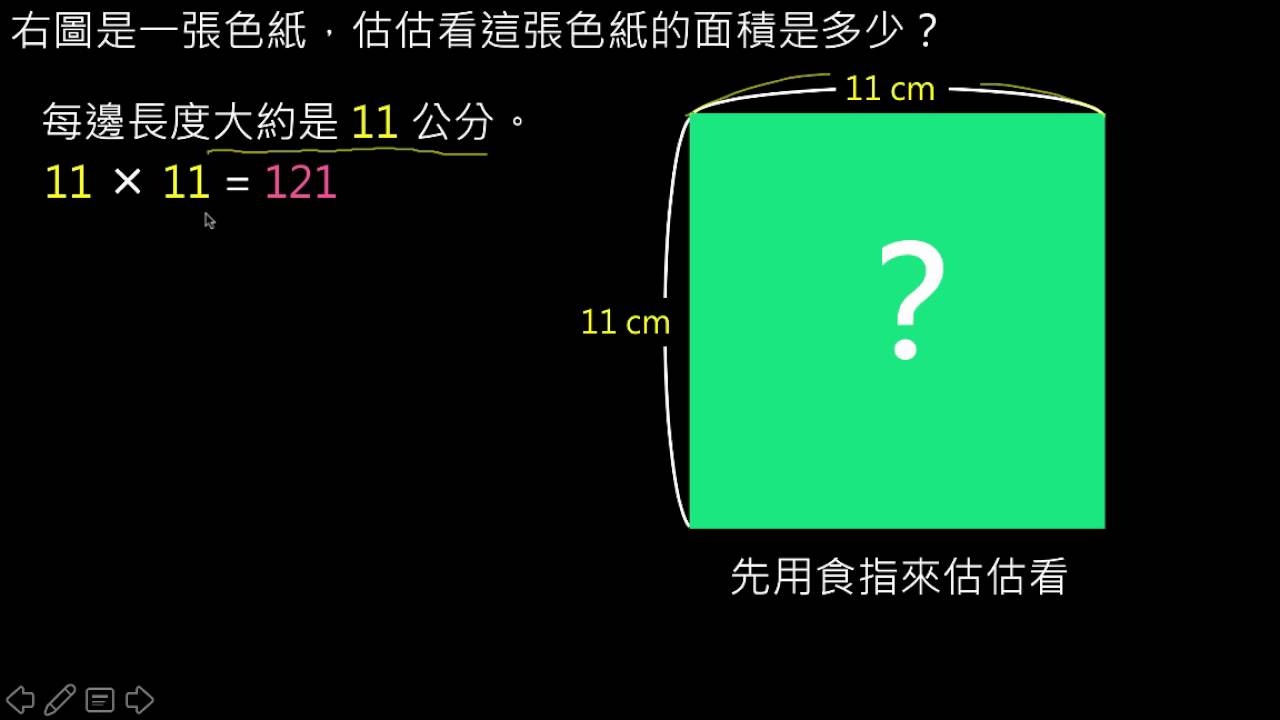
正方形，顾名思义，是具有四个相等边长和四个直角的平面几何图形。求解正方形的面积，最基础也是最常用的方法是利用其边长的平方。公式表达为：S = a²，其中S代表正方形的面积，a代表正方形的边长。

这个公式的推导可以从多个角度理解。首先，我们可以将正方形分割成多个更小的正方形，例如，边长为a的正方形可以分割成a×a个边长为1的小正方形。这些小正方形的面积之和，自然就是大正方形的面积，即a×a=a²。

其次，从代数几何的角度，我们可以将正方形视为一个特殊的矩形，其长和宽都相等。而矩形的面积公式为：S=ab，其中a为长，b为宽。当a=b时，即为正方形，公式便简化为S=a²。

理解公式推导的过程，有助于我们更深刻地掌握正方形面积计算的本质，避免单纯的公式套用而忽略其背后的几何意义。例如，在实际测量中，我们可以通过测量正方形的一条边长，然后直接利用公式计算其面积，快速高效。

正方形面积计算在生活中的实际应用

正方形面积的计算方法并非仅仅存在于数学课本中，它广泛应用于生活的方方面面。

例如，在装修房屋时，需要计算瓷砖、地板等材料的用量，这时正方形面积的计算就显得尤为重要。假设要铺设一块边长为50厘米的正方形瓷砖，那么一块瓷砖的面积就是50cm * 50cm = 2500平方厘米。通过计算房间的面积，就可以估算出所需瓷砖的数量，避免材料浪费。

再比如，在农业生产中，计算田地的面积也离不开正方形面积的计算。许多田地被规划成近似正方形的形状，通过测量田地的边长，农民可以快速计算出田地的面积，从而更好地安排种植计划，提高生产效率。

此外，在工程建设中，正方形面积的计算也扮演着重要的角色。例如，计算建筑物的地基面积、计算需要铺设的道路面积等等，都需要运用到正方形面积的计算方法。

正方形面积计算的常见问题与误区

在实际应用中，正方形面积的计算虽然简单，但也存在一些常见的问题和误区。

首先，单位换算是一个容易出错的地方。例如，如果边长用米来计算，那么面积的单位就是平方米；如果边长用厘米来计算，那么面积的单位就是平方厘米。如果不注意单位换算，很容易导致计算结果出错。

其次，在测量边长时，需要保证测量的精度。如果测量误差过大，那么计算出来的面积也会存在较大的偏差。建议在测量时使用精度较高的工具，并多次测量取平均值，以降低误差。

最后，对于一些形状不规则的图形，不能直接套用正方形面积的计算公式。例如，如果图形是近似正方形的，需要根据实际情况进行处理，可以选择将图形分割成若干个更小的正方形或矩形，分别计算面积后求和。

正方形面积计算方法的未来发展趋势及展望

随着科技的进步，正方形面积的计算方法也将会不断发展。

未来，人工智能和自动化技术的发展可能会为正方形面积的计算提供更便捷、更精准的工具。例如，利用图像识别技术，可以自动识别和测量任意形状的图形的边长，从而自动计算其面积。这将极大地提高计算效率，并减少人为误差。

同时，一些更加高效的算法可能会被开发出来，以提高正方形面积计算的速度和精度。这些算法可能会结合其他数学方法，例如微积分或线性代数等，以处理更复杂的图形和计算场景。

总而言之，正方形面积计算方法将会在未来不断发展，成为更加智能化、自动化、高精度的计算工具，服务于各个领域。