轻松掌握：水平渐近线怎么求？详解求解方法及应用技巧

本文系统讲解了水平渐近线怎么求，从概念理解到求解方法，再到不同类型函数的求解技巧及实际应用，并分析了常见的误区。掌握水平渐近线的求解方法对于理解函数图像和解决实际问题具有重要意义。文章中提到的极限法、不同类型函数的求解技巧以及实际应用案例，都能够帮助读者更好地理解和掌握水平渐近线的求解方法，并将其应用于实际问题中。

理解水平渐近线的概念及意义

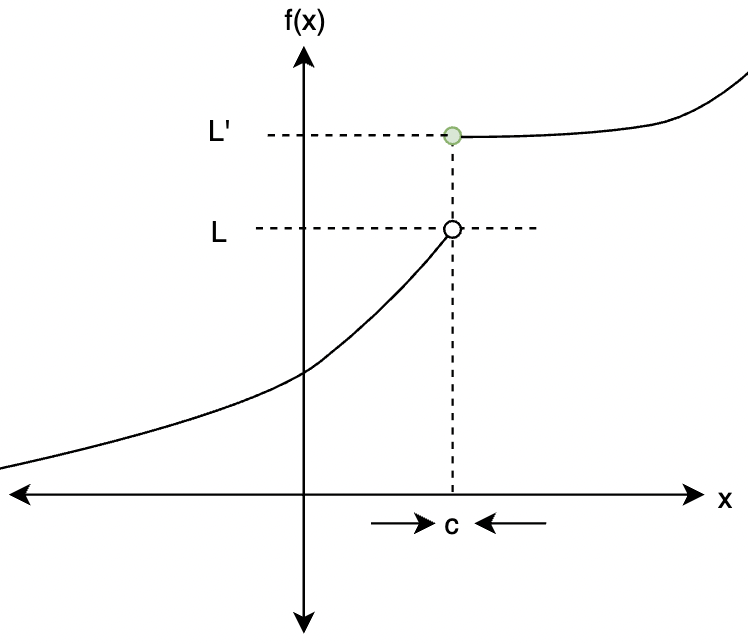
水平渐近线描述的是函数图像在x趋于正无穷或负无穷时，y值所趋近的常数。理解其概念是求解的关键。当一个函数在x无限增大或减小时，其图像无限接近于一条水平直线，这条直线就叫做水平渐近线。

例如，函数f(x) = 1/x，当x趋于正无穷或负无穷时，f(x)的值无限接近于0，所以y=0是函数f(x) = 1/x的水平渐近线。理解水平渐近线的意义在于它可以帮助我们了解函数图像的整体走势，特别是当x取值很大时，函数值的变化趋势。这在分析函数的增长速度和长期行为时非常重要，例如在经济学中分析长期投资收益，以及物理学中分析粒子运动的渐近行为等。

在实际应用中，例如研究人口增长模型，我们可以利用水平渐近线来预测人口数量的最终稳定值；在化学反应动力学中，水平渐近线可以表示反应速率的最终稳定值。这些应用都体现了水平渐近线在解决实际问题中的重要作用。

求解水平渐近线的常用方法：极限法

求解水平渐近线最常用的方法是利用极限的思想。具体来说，我们需要计算函数在x趋于正无穷和负无穷时的极限。如果极限存在且为一个常数c，那么y=c就是函数的水平渐近线。

例如，对于函数f(x) = (2x + 1)/(x - 1)，我们可以通过计算极限lim(x→∞) f(x) 和lim(x→-∞) f(x) 来求解水平渐近线。使用洛必达法则或直接分析分子分母最高次项的系数比值，我们可以得到极限值为2，因此y = 2是该函数的水平渐近线。

需要注意的是，并不是所有函数都存在水平渐近线。如果极限不存在，或者极限为无穷大，那么该函数就没有水平渐近线。例如，函数f(x) = x²就没有水平渐近线，因为它在x趋于正无穷或负无穷时，极限为无穷大。掌握极限的计算方法对于准确求解水平渐近线至关重要，这需要熟练运用极限运算法则，例如洛必达法则等。

不同类型函数水平渐近线的求解技巧

不同类型的函数，求解水平渐近线的方法略有不同。对于分式函数，我们可以直接比较分子和分母最高次项系数的比值来快速求解。对于指数函数和对数函数，则需要根据其函数特性，结合极限的计算方法来确定水平渐近线。

例如，对于指数函数f(x) = e^x，当x趋于负无穷时，极限为0，所以y = 0是其水平渐近线；而对于对数函数f(x) = ln(x)，当x趋于正无穷时，极限为无穷大，因此它没有水平渐近线。

对于一些较为复杂的函数，可能需要运用多种方法结合，例如先进行函数化简，再利用极限法求解。在求解过程中，需要仔细分析函数的性质和图像特征，才能准确地确定水平渐近线的存在性和位置。熟练掌握不同类型函数的特性，是提高水平渐近线求解效率的关键。

水平渐近线求解的实际应用及误区分析

• 在经济学模型中，用于预测长期经济指标的稳定值，例如长期经济增长率。
• 在物理学中，用于描述粒子运动的渐近行为，例如物体的终端速度。
• 在化学动力学中，用于分析反应速率的最终稳定值。
• 在生物学中，用于分析种群数量的长期变化趋势，例如环境容纳量。
• 在工程学中，用于分析系统稳定性，例如控制系统的稳定性分析。