最大公因数怎么求？详解多种算法及应用场景

本文详细介绍了如何求最大公因数，涵盖了辗转相除法、更相减损术等多种算法，并分析了其应用场景及未来发展趋势。掌握这些方法，可以帮助我们更好地理解和应用最大公因数，解决实际问题，例如分数化简、几何计算等，更能提升对于数学算法的理解。

最大公因数的概念与理解

最大公因数，简称最大公约数，指能够同时整除若干整数的最大正整数。理解最大公因数的关键在于认识“公约数”和“最大”这两个概念。公约数指的是能够同时整除这几个数的整数，而最大公因数则是在所有这些公约数中最大的一个。例如，求6和9的最大公因数。6的约数有1,2,3,6；9的约数有1,3,9。6和9的公约数是1和3，其中最大的公约数是3，因此6和9的最大公因数为3。理解最大公因数的概念是掌握其计算方法的第一步，也是解决实际问题的重要基础。

在实际应用中，最大公因数常用于化简分数、解决比例问题以及一些几何图形的计算中。例如，在化简分数时，分子和分母的最大公因数可以用来约分，得到最简分数。

在学习最大公因数的过程中，很多学生容易混淆最大公因数与最小公倍数的概念。最小公倍数指的是能够同时被若干整数整除的最小正整数。记住，最大公因数是“最大”，最小公倍数是“最小”，区分这两个关键词能够帮助我们更清晰地理解两者之间的区别。

辗转相除法求最大公因数

辗转相除法，也称欧几里德算法，是求最大公因数最常用的方法之一。它的核心思想是利用除法，不断用较大的数除以较小的数，直到余数为0。最后的除数就是这两个数的最大公因数。例如，求12和18的最大公因数。

首先，18 ÷ 12 = 1……6；然后，12 ÷ 6 = 2……0。因为余数为0，所以最后的除数6就是12和18的最大公因数。

辗转相除法的优点是算法简单、高效，适合求解较大数字的最大公因数。它的原理基于这样一个数学事实：两个数的最大公因数等于其中较小的数和余数的最大公因数。通过不断重复这个过程，最终可以得到这两个数的最大公因数。

然而，辗转相除法也存在一些局限性，例如当数字非常大时，计算过程可能会比较复杂。而且，它只适用于求解两个数的最大公因数，对于多个数求最大公因数，需要多次使用该算法。

更相减损术求最大公因数

更相减损术是我国古代数学家提出的求最大公因数的方法。它的核心思想是利用减法，不断用较大的数减去较小的数，直到两个数相等，这个相等的数就是最大公因数。例如，求12和18的最大公因数。

首先，18 - 12 = 6；然后，12 - 6 = 6。因为两个数都变成了6，所以6就是12和18的最大公因数。

更相减损术的优点是算法简单易懂，不需要进行除法运算，在古代计算工具有限的情况下，更相减损术具有很大的优势。然而，更相减损术的计算效率相对较低，尤其当两个数相差较大时，需要进行多次减法运算。而且，更相减损术与辗转相除法一样，也主要适用于求解两个数的最大公因数。

短除法求多个数的最大公因数

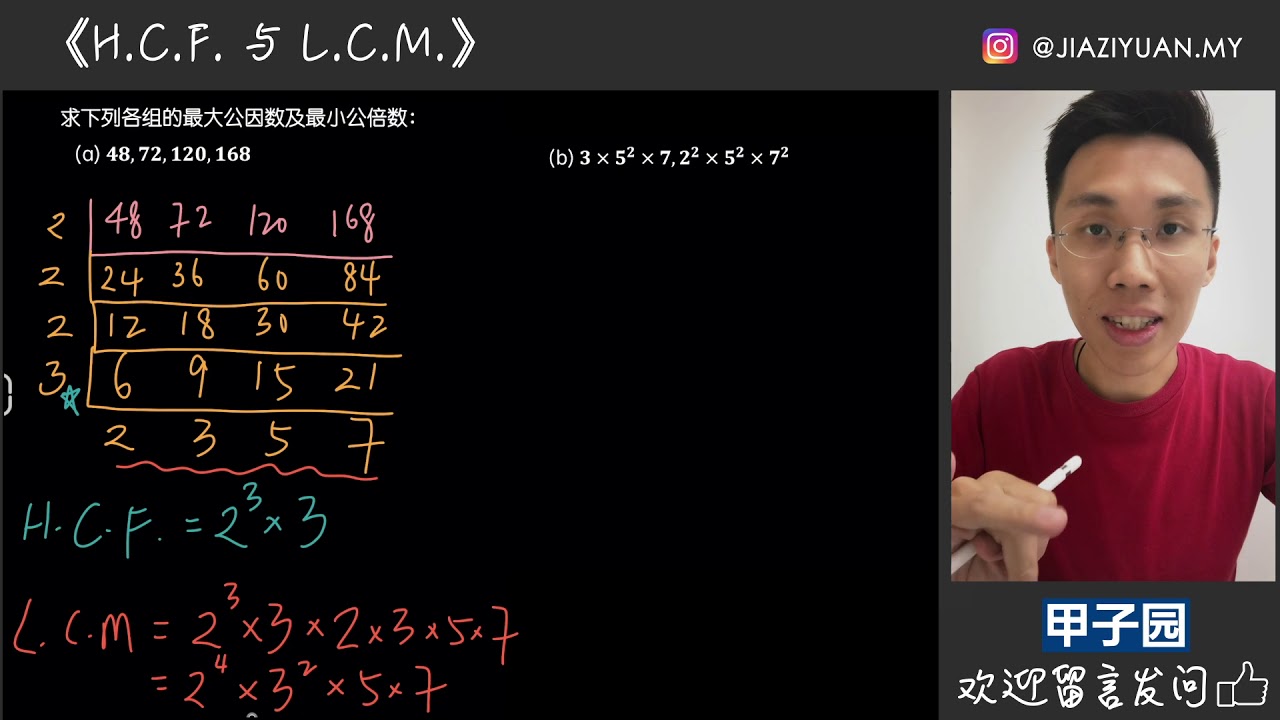
• 将所有待求最大公因数的数按从小到大的顺序排列。
• 选取最小的数，用它去除其余所有数。
• 若有余数，则将余数和去除数进行辗转相除。
• 重复上述步骤，直到所有的数都被约简到没有公因数为止。
• 最后剩下的数的乘积，即为这些数的最大公因数。

最大公因数的实际应用与未来展望

最大公因数的应用广泛存在于我们的日常生活中，例如在分数的化简、几何问题的计算中都扮演着重要的角色。在计算机科学中，最大公因数算法被广泛应用于密码学、数据压缩等领域。例如，在RSA加密算法中，最大公因数的计算是关键步骤之一。

随着计算机技术的发展，对更大规模数字进行最大公因数计算的需求也越来越大。未来，研究更高效、更快速的算法，以及在量子计算等新兴计算模式下研究最大公因数算法，将会是重要的研究方向。尤其是在数据安全和数据处理领域，更高效的算法能带来显著的性能提升。

目前，已有许多研究者在探索更优化的最大公因数算法，并取得了显著进展。例如，针对特定类型数字的最大公因数计算，已经开发出一些具有更高效率的算法。预计未来会有更多针对不同场景的算法被开发出来，以满足不断增长的计算需求。