半圆周长计算公式详解：从基础概念到实际应用及误区分析

本文深入浅出地讲解了半圆的周长计算方法，从基本公式到实际应用，并分析了常见的误区。文章指出，准确计算半圆周长需要理解公式的推导过程，并结合实际情况灵活运用。在实际应用中，半圆周长计算广泛应用于建筑、园林、机械制造等领域，掌握该计算方法具有重要意义。通过本文的学习，读者可以更好地理解并掌握半圆周长计算方法，在实际生活中运用自如。

理解半圆周长的基本概念

半圆的周长，顾名思义，就是半圆形的周长。它包含两部分：一段圆弧和一条直径。计算半圆周长，需要我们充分理解圆的周长计算公式：C = 2πr，其中r代表圆的半径，π约等于3.14159。由于半圆只占圆周的一半，因此半圆的弧长为： (2πr)/2 = πr。

那么，半圆的周长就等于弧长加上直径，即：πr + 2r = r(π+2)。

这个公式是计算半圆周长的基础。但实际应用中，我们可能遇到的情况并非总是已知半径。例如，如果只知道半圆的直径，我们可以用直径除以2得到半径，再代入公式计算。又或者，如果题目只给出了半圆的面积，则需要先根据面积公式求出半径，再进行周长计算。

理解这些变化，才能灵活运用公式，解决各种类型的半圆周长计算问题。 许多几何题都涉及到半圆周长的计算，掌握这个基础概念十分重要。例如，计算半圆形花坛的围栏长度、计算半圆形拱桥的桥拱长度，都需要用到这个公式。

不同已知条件下的半圆周长计算

• 已知半径r，直接套用公式r(π+2)进行计算。
• 已知直径d，先计算半径r=d/2，再套用公式r(π+2)。
• 已知面积A，根据半圆面积公式A = πr²/2求出半径r，再套用公式r(π+2)。
• 已知弧长l，则半圆的半径为r=l/π，然后套用公式r(π+2)。
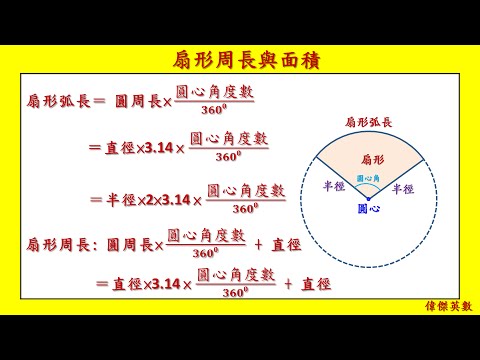
• 已知圆弧的度数和半径，例如：已知半圆弧的度数为180°，可以先根据角度求出半圆弧长l=（180°/360°）*2πr=πr，然后计算周长πr+2r。

半圆周长计算在实际生活中的应用

半圆周长的计算并非仅仅局限于数学课堂上的理论问题，它广泛应用于许多实际领域。

例如，在建筑工程中，计算半圆形拱桥的长度、半圆形屋顶的周长都需要用到半圆周长公式。工程师们需要精确计算这些数据，才能确保建筑的稳定性和美观性。

在园林设计中，设计师们也常常需要计算半圆形花坛、喷泉的周长，来确定所需材料的用量。

此外，在机械制造、服装设计等领域，半圆周长的计算也发挥着重要的作用。例如，设计一个半圆形的零件，需要精确计算其周长，才能保证零件的精度和功能。

总而言之，半圆周长计算在许多实际问题中都有着广泛的应用，掌握这一计算方法具有重要的实际意义。

半圆周长计算中的常见误区及注意事项

在半圆周长的计算中，一些常见的误区需要引起我们的注意。

首先，许多人容易忽略半圆周长包含直径这一部分，只计算弧长而忽略了直线部分，导致计算结果错误。

其次，在使用公式时，要注意单位的一致性。如果半径的单位是厘米，那么计算出来的周长也应该是厘米，切忌单位混淆导致错误。

再次，对于一些复杂的半圆组合图形，需要先将图形分解成简单的几何图形，分别计算周长，再进行求和，避免漏算或重复计算。

最后，在进行实际测量时，要尽可能保证测量的精确性，避免由于测量误差导致计算结果出现较大偏差。

总之，在进行半圆周长计算时，要认真仔细，避免这些常见的误区，才能保证计算结果的准确性。