360度的角怎么画？详解几何作图及实际应用

本文详细阐述了如何理解和“绘制”360度角，从几何作图到实际应用，涵盖了360度角的几何意义、作图方法以及在不同领域（例如，工程制图、钟表等）的应用案例。文章深入探讨了360度角在不同学科中的解读与应用，例如数学、物理学和计算机图形学。通过学习本文，读者能够更加全面地理解360度角的概念，并掌握其在实际生活中的应用方法。

理解360度角的概念及几何意义

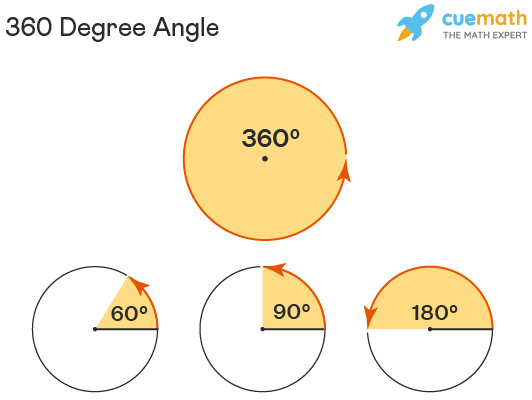
要画一个360度的角，首先要理解其几何意义。360度角实际上是一个完整的圆周，它代表一个点绕另一点旋转一周所形成的角度。理解这一点至关重要，因为它直接决定了我们作图的思路。

从几何学的角度来看，360度角并非一个普通的角，它是一个特殊的角，代表了周而复始的概念。它不同于小于360度的角，后者有明确的起始边和终止边。而360度角的起始边和终止边重合，构成一个封闭的图形——圆。

我们可以将360度角理解为一个完整的循环过程。例如，地球自转一周是360度，钟表指针走完一圈也是360度。这种循环的概念在许多领域都有应用，例如机械工程、电子技术等等。

在实际作图中，我们通常不会直接画一个完整的360度角，因为完整的圆本身就代表了360度。因此，我们更关注的是如何理解和应用360度角的概念，以及如何在实际应用中运用这个概念进行相关的计算和推导。

360度角的作图方法：利用圆规和直尺

虽然我们不能直接画出一个“角”来表示360度，但我们可以用圆来表示。用圆规和直尺作图，是几何作图中最基础也是最常用的方法。

首先，我们需要一个圆心。选择一个点作为圆心，用圆规在纸上画一个圆。这个圆的周长就代表了360度。我们可以用圆规任意设定半径，这不会影响360度角的表示，因为一个圆的周长与半径成正比，而我们关注的是这个圆完整的周长代表的意义。

绘制圆的过程中，需要注意的是保证圆规的张角不变，确保画出的圆是标准的圆形。如果圆规的张角变化，那么画出的圆将会变形，这就会影响到对360度角的精准表示。

实际上，画圆本身就完成了360度角的“绘制”过程。圆本身就是一个360度角的形象化表达。我们不需要刻意地去标注角度，圆本身就蕴含着360度的信息。

除了圆规和直尺，现代技术也提供了更加便捷的方法。例如，借助专业的制图软件，可以快速精确地绘制圆形，从而表示360度角。

360度角在实际生活中的应用案例

• 在钟表上，时针和分针走完一圈都是360度。
• 地球自转一周是360度，构成了我们昼夜交替的循环。
• 在工程制图中，360度角常用于表示圆形零件的尺寸和形状。
• 在计算机图形学中，360度角被广泛应用于三维建模和动画制作。
• 在轮子的旋转过程中，也隐含着360度的概念，它代表着轮子的一次完整旋转。

360度角在不同学科中的解读与应用

360度角的概念在不同学科领域有着不同的解读和应用。在数学中，它是圆周角的完整表达，是三角函数、几何计算的基础；在物理学中，它可以用来描述旋转运动，例如描述一个物体的角速度和角加速度。

在工程学中，360度角广泛应用于机械设计、建筑设计等领域，例如设计圆形零件、计算旋转部件的运动轨迹等等。 在导航领域，方向的表示也常常基于360度角的坐标系。一个物体相对于参考点360度旋转后回到原点，这在方向测算中非常重要。

此外，在计算机图形学中，360度角是三维建模和动画制作的基础。游戏角色、建筑模型的旋转都是基于对360度角的精准计算和控制。例如，一个虚拟摄像机绕着物体旋转一圈，就是基于360度角来完成的。

总而言之，尽管我们不直接画“360度角”，但对它的理解贯穿各个领域，体现了数学概念在实践中的应用广泛性，提升了我们对于旋转、周期性现象的认识能力。