怎么脱式计算？详解脱式计算的步骤、技巧及常见错误

本文详细阐述了怎么脱式计算，从基本步骤到常见错误，再到提高效率的策略，深入浅出地讲解了脱式计算的方方面面。文章涵盖了脱式计算的步骤、不同类型脱式计算的解题技巧以及如何提高计算效率等内容，并分析了脱式计算中常见的错误及预防方法，旨在帮助读者更好地理解和掌握脱式计算。学习如何进行分数小数的脱式计算和掌握混合运算的脱式计算是提升数学能力的关键。

脱式计算的基本步骤与顺序

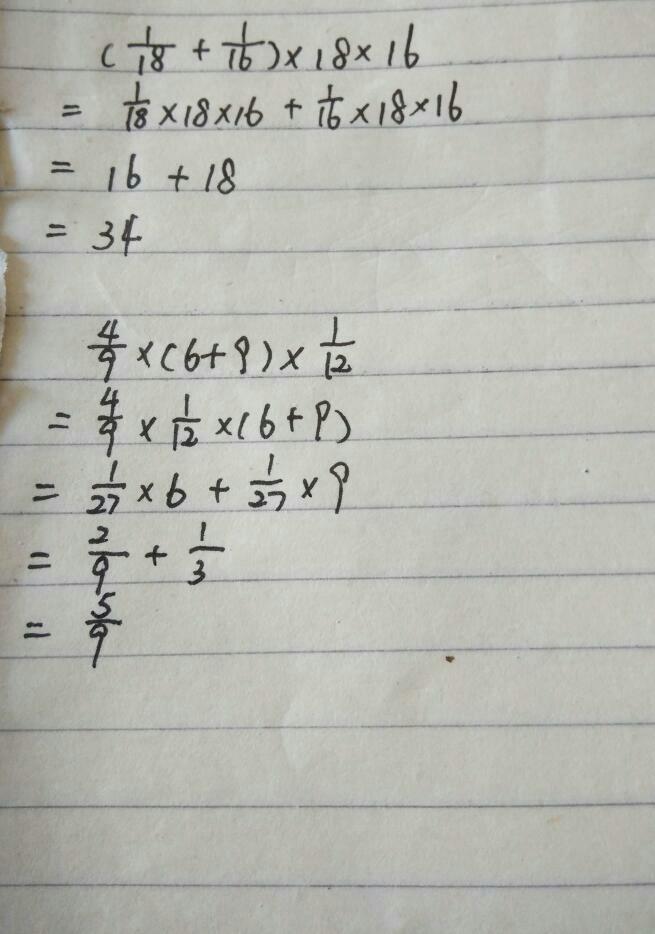
脱式计算是数学运算中一项重要的技能，它指的是按照一定的运算顺序进行计算，而不是一步一步地进行计算。掌握脱式计算的关键在于理解运算顺序，这通常遵循以下几个步骤：

第一步，明确运算顺序。通常情况下，先算括号里的，再算乘除，最后算加减。如果有相同的运算符，则从左到右依次计算。例如：10 + 2 × 3 = 10 + 6 = 16， 这里先计算2 × 3。

第二步，认真审题。要仔细阅读题目，弄清楚运算符号和数字，避免看错题或抄错题，出现不必要的错误。比如：题目中括号的类型，是圆括号还是方括号，这会影响运算顺序。

第三步，按步骤计算。计算时，应一步一步地进行，写出每一步的计算过程，以便检查和纠错。例如，在计算含有分数或小数的脱式计算时，要特别注意小数点的位置以及分数的通分等问题。

第四步，检查结果。计算完毕后，要认真检查计算结果是否正确，是否有笔误或者计算错误。可以尝试用不同的方法重新计算一遍，或者用计算器验证结果。例如，计算结果是否合理，是否符合实际情况。

学习脱式计算需要反复练习，多做题才能更好地掌握其技巧。熟练掌握运算顺序，认真审题，并养成良好的计算习惯，对于提高数学运算能力至关重要。许多学生在脱式计算时容易出现粗心大意的情况，因此认真细致是关键。

不同类型的脱式计算及解题技巧

脱式计算的题型多种多样，根据运算符号和数字的不同，可以分为很多类型，例如：含有括号的脱式计算、含有分数或小数的脱式计算、含有混合运算的脱式计算等等。

对于含有括号的脱式计算，一定要先计算括号里面的算式，再计算括号外面的算式。如果括号有多层，则需要从内层到外层依次计算。例如，{(2+3)×4+1}=21。

含有分数或小数的脱式计算，需要注意分数或小数的运算规则。分数的加减法需要通分，乘除法则直接进行计算；小数的加减法需要注意小数点对齐，乘除法则需要注意小数点位数的计算。例如，计算1/2 + 1/3，需要先通分变为3/6 + 2/6 = 5/6。

对于含有混合运算的脱式计算，需要按照先乘除后加减的规则进行运算。如果遇到多个相同的运算符，则需要从左到右依次计算。例如，2+4×6-3=23。

总之，面对不同的脱式计算题型，需要灵活运用不同的解题技巧，并熟练掌握各种运算规则。准确理解运算顺序和运算规则，是做好脱式计算的关键。

脱式计算中常见的错误及预防方法

在脱式计算的过程中，学生们常常会犯一些常见的错误，这些错误通常是因为对运算顺序理解不清、计算粗心大意或者运算规则运用不当所导致的。

例如，一些学生会忽略括号的作用，或者没有按照正确的运算顺序进行计算。还有的学生在进行分数或小数运算时，容易出现小数点错位或分数通分错误等问题。此外，在进行混合运算时，也容易出现运算顺序颠倒等问题。

为了避免这些错误，学生们需要认真学习运算顺序和各种运算规则，并且在计算过程中要细心，一步一步地进行计算，并且要养成检查计算结果的良好习惯。可以尝试使用不同的计算方法来验证结果，确保计算的准确性。例如，可以用计算器进行验算，或者用估算的方法来判断结果是否合理。

老师在教学过程中，也应该重视学生对运算顺序的理解，并引导学生养成良好的计算习惯。可以设计一些针对性练习，帮助学生巩固知识点，并提高计算能力。

提高脱式计算效率的策略与方法

• 合理安排计算顺序，避免重复计算。
• 熟记一些常用的计算技巧和公式。
• 利用简便方法进行计算，例如运用乘法分配律。
• 多练习，提高计算速度和准确率。
• 在练习过程中，注意分析错误，总结经验教训。
• 掌握多种解题方法，并根据实际情况选择最合适的解题方法。
• 利用计算器等工具辅助计算，但要避免依赖计算器。
• 保持良好的心态，避免因紧张或急躁而出现计算错误。
• 在计算过程中要保持清晰的思路，避免思维混乱。
• 加强基础知识的学习，为提高脱式计算能力打下坚实的基础。

脱式计算的未来发展趋势及展望

随着人工智能和信息技术的不断发展，未来脱式计算的学习和应用方式可能会发生一些变化。例如，人工智能技术可以提供个性化的学习指导，帮助学生更好地掌握脱式计算的技巧。同时，一些在线学习平台可以提供丰富的脱式计算练习题和练习工具，方便学生进行学习和练习。

此外，未来在教学中，可能会更加强调对学生数学思维的培养，而不是仅仅关注计算结果的正确性。例如，注重培养学生的逻辑推理能力、问题解决能力和创造性思维。

虽然技术可能会改变学习方式，但是掌握扎实的运算基础、熟练运用运算规则以及养成良好的计算习惯依然是进行脱式计算的关键。未来，脱式计算的学习和应用仍然会持续受到重视，因为它是学生掌握数学和其他科学知识的基础。