怎么拟合曲线：从基本原理到实际应用的全面分析

怎么拟合曲线是一个复杂的问题，它包括了多种方法和技术。最小二方法和回归算法是两种常用的方法，但其它方法也可以应用。选择哪种方法，要结合实际情况和拟合目的。拟合曲线应用广泛，在多个领域都有应用。

拟合曲线的基本原理

拟合曲线是一种重要的数据分析技术，它的基本原理是在给定的数据集中，找到一条最为一致的曲线来表现这些数据之间的规律。这条曲线可以是一条简单的直线，也可以是一条复杂的函数曲线，这取决于数据的特点和拟合的目的。在实际应用中，常用的拟合方法包括最小平方法、最小二方法、回归算法等。例如，在制造产品过程中，可以通过拟合曲线来控制产品的品质。再如，在财币领域，可以通过拟合曲线来预测财币市场的趋势。

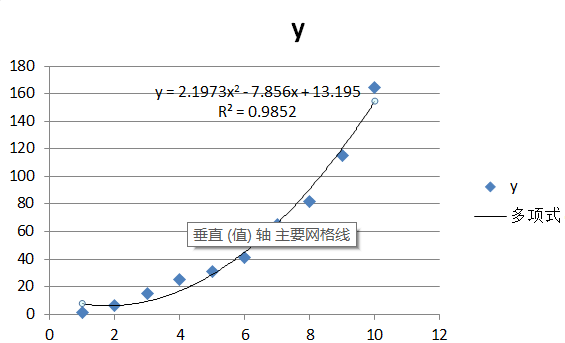
各种拟合方法的特点和选择

在实际工作中，我们常用的拟合方法很多，例如简单的直线拟合，到雅重的多项式拟合，甚至使用神经网络拟合曲线。不同的方法具有不同的优缺点。简单方法运算速度快，但精度较低；雅重方法精度高，但运算难度增加。选择什么方法，要结合实际情况和拟合目的进行恰当的选择。根据数据的特点，选择合适的模型方法，才能得到最佳的拟合结果。如果数据中包含多个关键变量，则需要选择多项式模型方法。

拟合曲线的应用场景

拟合曲线在很多领域都有应用，例如医学领域，可以通过拟合曲线来分析病人的生理活动指标，帮助医生诊断和治疗；在科学研究中，可以通过拟合曲线来找出变量之间的规律和关系；在工程设计中，可以通过拟合曲线来设计和保证工程的安全性和稳定性。所以，拟合曲线的应用很广，其应用领域仍在扩展中。

拟合曲线的优缺点及将来发展趋势

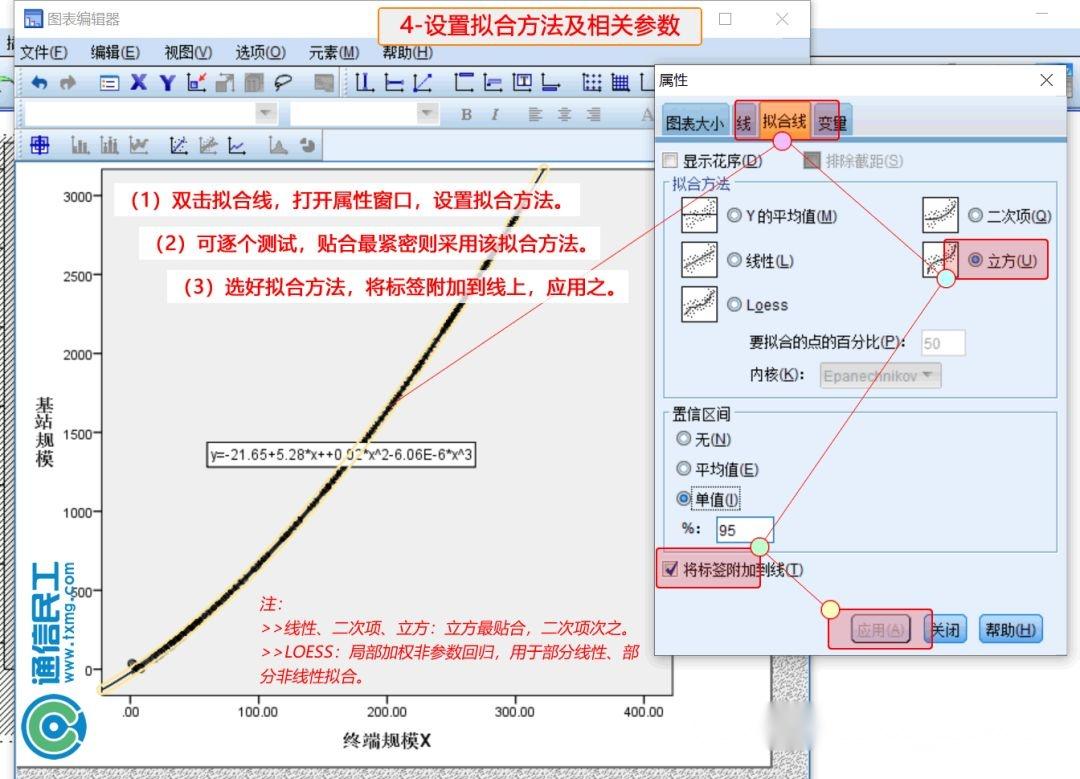
• 优点：它可以将数据表现在一条曲线上，使数据更加完整和明亮。
• 它可以预测和预计数据的变化趋势。
• 它可以帮助我们理解数据之间的关系。
• 它应用广泛，在多个领域都有应用。
• 它的技术在一直前进，对数据分析有重要意义。