正态分布最新研究：从理论到应用的深入探讨及未来展望

本文探讨了正态分布最新的研究进展，从其在机器学习中的应用扩展，到高维数据处理中的挑战与机遇，再到非正态分布数据的处理方法以及未来的发展趋势，都进行了深入浅出的分析。文章指出，正态分布的应用范围不断扩大，但同时也面临着新的挑战，例如高维数据和非正态分布数据的处理。未来，正态分布的研究方向将更加注重理论与应用的融合，开发更加高效和稳健的统计方法和模型。

正态分布的应用扩展：从经典统计到机器学习

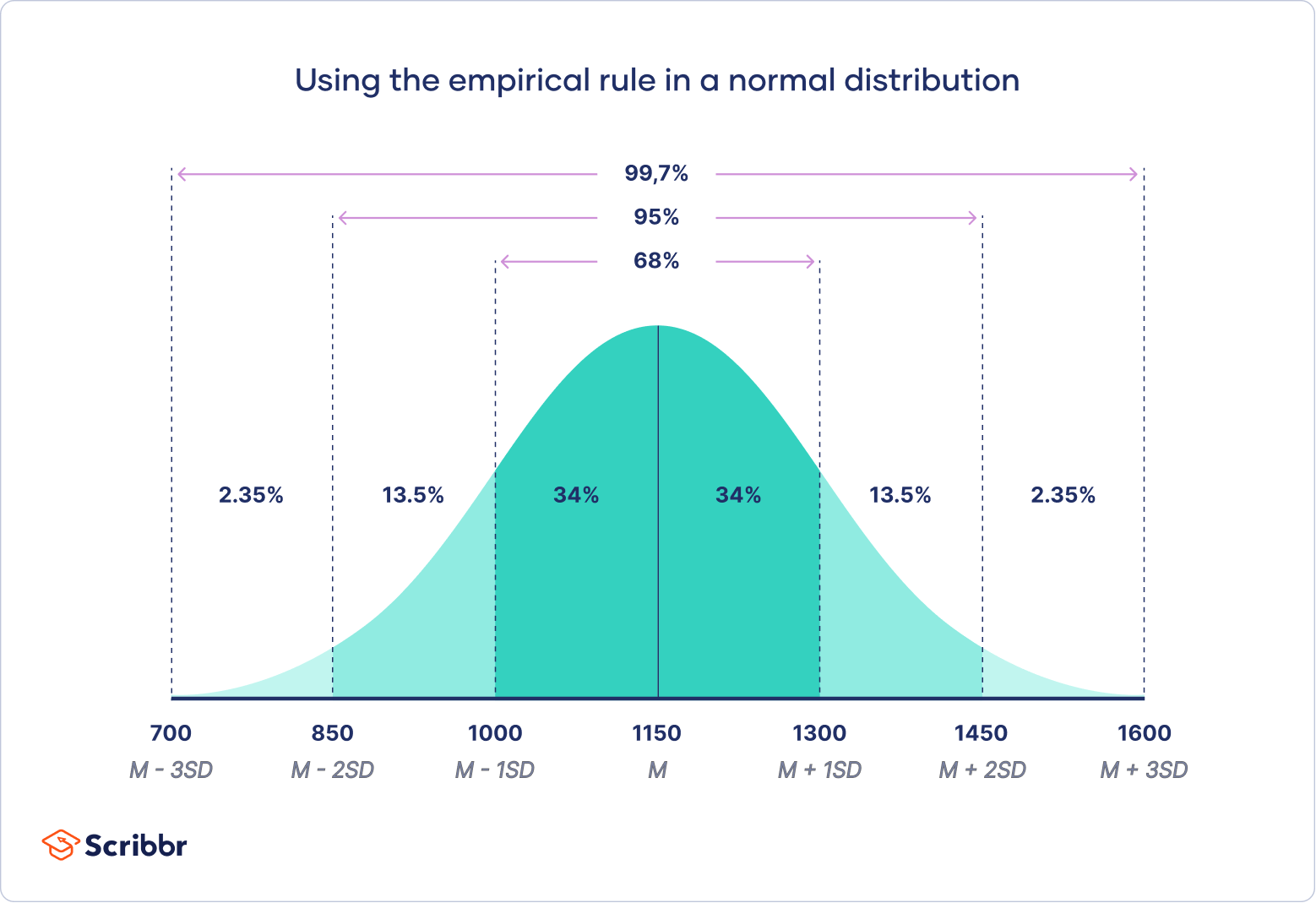
正态分布，作为统计学中的基石，其应用早已超越了传统的统计分析领域。

近年来，随着机器学习和人工智能的快速发展，正态分布在这些新兴领域中也扮演着越来越重要的角色。

例如，在高斯过程回归中，正态分布被用来建模预测的不确定性；在许多概率模型中，例如隐马尔可夫模型，也广泛应用正态分布假设。

此外，一些基于正态分布假设的算法，例如线性判别分析（LDA）和高斯混合模型（GMM），在模式识别和聚类分析等领域也取得了显著成果。

然而，实际应用中，数据往往并不完全符合正态分布假设。因此，如何处理非正态分布数据，并充分利用正态分布的优势，成为一个重要的研究方向。

一些研究者提出了一些改进方法，例如数据变换、稳健统计方法等，以减轻非正态分布数据对模型的影响。

总而言之，正态分布的应用正在不断扩展，其在机器学习和人工智能领域的应用将会持续发展，并催生更多新的理论和方法。

高维数据处理中的正态分布：挑战与机遇

随着大数据时代的到来，高维数据处理成为一个日益重要的课题。

在高维数据中，正态分布的性质和应用面临着新的挑战。

例如，在高维空间中，正态分布的概率密度函数会变得非常扁平，这使得传统的基于正态分布假设的统计方法在高维数据中往往表现不佳。

此外，高维数据中的噪声和冗余信息也会对正态分布的估计造成影响。

为了解决这些问题，研究者们提出了许多新的方法，例如降维技术、稀疏学习等。

这些方法旨在降低数据的维数，去除噪声和冗余信息，从而提高正态分布估计的精度。

同时，高维数据也为正态分布的研究提供了新的机遇。

一些研究者发现，在某些高维数据中，数据的分布仍然近似服从正态分布，这为基于正态分布假设的统计方法在高维数据中应用提供了理论基础。

总之，高维数据处理中的正态分布既面临着挑战，也蕴含着机遇。未来，如何更好地利用正态分布的性质，解决高维数据处理中的问题，将是一个重要的研究方向。

非正态分布数据的处理方法：超越正态性假设

在实际应用中，许多数据的分布并不完全服从正态分布，例如金融数据、环境数据等往往呈现出明显的偏态或厚尾特征。

对于这些非正态分布的数据，直接应用基于正态分布假设的统计方法可能会导致结果不准确，甚至产生错误的结论。

因此，如何处理非正态分布的数据，成为一个重要的研究问题。

目前，常用的处理方法包括：数据变换，如对数变换、Box-Cox变换等，将非正态分布数据转化为近似正态分布的数据；

稳健统计方法，如中位数、四分位数间距等，减少异常值对统计结果的影响；

非参数统计方法，如秩检验、核密度估计等，无需对数据分布做出特定的假设。

此外，一些新的统计模型和方法也在不断涌现，例如copula模型，可以对多元非正态分布数据进行建模。

这些方法的应用，极大地拓展了正态分布的应用范围，提高了统计分析的准确性和可靠性。

选择合适的处理方法需要根据数据的具体特性和分析目标进行判断。

正态分布的未来发展趋势：理论与应用的融合

正态分布作为概率论和数理统计的重要组成部分，其理论和应用都在不断发展。

未来，正态分布的研究方向可能包括：

更深入地研究正态分布在高维数据、复杂网络等领域的应用；

发展更加稳健和高效的非正态分布数据处理方法；

结合机器学习和人工智能技术，开发新的基于正态分布的统计模型和算法；

探索正态分布在其他交叉学科，例如生物信息学、金融工程等领域的应用。

同时，需要进一步探索正态分布的局限性，以及如何在实际应用中更好地解决这些局限性。

总而言之，正态分布的理论研究和实际应用将更加紧密地结合，不断推动统计学的发展，为解决实际问题提供更加有效的方法和工具。