本文详细讲解了最小公倍数的概念、计算方法(短除法和分解质因数法)以及在分数运算中的应用,并指出了计算中的误区和技巧。通过学习本文,读者可以掌握最小公倍数的计算方法,并能够将其应用于实际问题的解决,例如,解决分数加减、化简分数,以及一些生活中的比例问题,例如计算两个齿轮再次同时啮合需要的圈数,以及解决工程问题。
理解最小公倍数的概念及意义
最小公倍数,简称 LCM(Least Common Multiple),指的是几个整数的公倍数中最小的那一个。理解最小公倍数的概念非常重要,因为它在很多实际问题中都有应用,例如解决分数加减、化简分数、以及解决一些生活中的比例问题等。例如,两个齿轮的齿数分别为 12 和 18,那么它们再次同时啮合需要转动多少圈呢?这就需要用到最小公倍数的计算。求出 12 和 18 的最小公倍数,就可以知道它们同时啮合需要的最小圈数。
此外,最小公倍数在日常生活中的应用也十分广泛,比如在安排工作计划、确定活动周期等方面,都需要用到最小公倍数的计算方法。例如,工厂生产 A 产品的周期是 3 天,生产 B 产品的周期是 5 天,那么工厂同时生产 A 和 B 两种产品,需要多少天才能同时完成两个产品的生产周期呢?答案是这两个数的最小公倍数,也就是 15 天。
通过这些例子我们可以看出,最小公倍数的计算不仅仅局限于数学课堂,而是与我们的日常生活密切相关,掌握最小公倍数的计算方法能够帮助我们更好地解决生活中的实际问题。
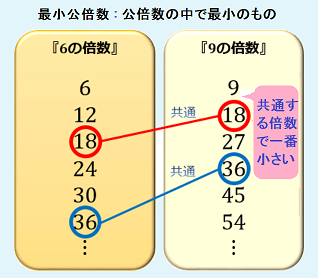
掌握两种常用的最小公倍数计算方法
求最小公倍数主要有两种方法:短除法和分解质因数法。短除法比较直观,适合求两个或多个整数的最小公倍数。具体步骤是:从最小的质数 2 开始,依次用质数去除这些数,直到商都是 1 为止。然后将所有用到的质数相乘,结果就是这些数的最小公倍数。例如,求 12、18 和 30 的最小公倍数:
2 | 12 18 30
3 | 6 9 15
3 | 2 3 5
| 2 1 5
5 | 2 1 5
| 2 1 1
最后将 2、3、3、5 相乘:2 × 3 × 3 × 5 = 90,所以 12、18 和 30 的最小公倍数是 90。
分解质因数法同样高效,尤其在处理较大数的时候优势更为明显。先将每个数分解成质因数的乘积形式,然后找出每个质因数的最高次幂,将这些最高次幂相乘,结果就是这些数的最小公倍数。例如,12 = 2² × 3,18 = 2 × 3²,则最小公倍数为 2² × 3² = 36。
最小公倍数在分数运算中的应用
- 化简分数:将分数化成最简分数时,需要用到最大公约数和最小公倍数。
- 通分:当进行分数加减法运算时,需要将分数通分,也就是将分数化为具有相同分母的分数,此时就需要用到最小公倍数。
- 分数比较大小:在比较分数大小时,如果分母不同,也可以先通分再进行比较,同样需要用到最小公倍数。
- 解决实际问题:例如,在工程问题、行程问题中,需要将时间或数量表示成分数进行运算,求解需要用到最小公倍数。
- 数学建模:在数学建模中,最小公倍数是重要的工具,可以用于解决一些实际问题,比如周期性的事件分析等等。
最小公倍数计算的误区及技巧
在计算最小公倍数的过程中,一些常见的误区需要注意:例如,不能简单地将几个数相乘作为最小公倍数,这往往会得到一个比实际最小公倍数更大的数;在使用短除法时,必须用质数去除,且要将每个数都除到1;在分解质因数时,要确保每个数都分解成质因数的乘积。
一些小技巧可以提高计算效率:熟练掌握 2-10 之间整数的质因数分解,能够加快计算速度;在分解质因数时,可以采用逐步分解的方法,从小到大进行质数试除,可以有效降低出错的可能性;对于较大的数字,可以考虑使用计算机或计算器来辅助计算,以提高准确性和效率。
此外,在实际运用中,理解题意,找出题目中隐含的条件,才能正确选择最小公倍数的计算方法,例如,工程问题通常需要求最小公倍数。







 鄂ICP备15020274号-1
鄂ICP备15020274号-1