根号3等于多少怎么算？详解根号3的计算方法及应用

本文详细阐述了根号3等于多少怎么算，涵盖了近似值计算、开方计算以及根号3在数学和实际生活中的应用，并分析了根号3计算误差和未来发展趋势。通过学习本文，读者可以掌握根号3的计算技巧，并理解其在不同领域的应用，例如，学习如何用牛顿迭代法求根号3的近似值，以及如何在实际工程中应用根号3进行计算。

根号3的近似值计算方法

根号3是一个无理数，它的值无法精确表示为有限小数或分数。但在实际应用中，我们常常需要使用根号3的近似值。

最常用的近似值是1.732。这个近似值可以利用计算器或计算机轻松得到。

此外，还可以通过一些简单的计算方法得到根号3的近似值，例如利用牛顿迭代法。牛顿迭代法是一种求解方程数值解的算法，可以用来计算根号3的近似值。具体方法是：先取一个初始值，例如1.5，然后根据迭代公式：x_(n+1) = (x_n + 3/x_n) / 2 进行迭代计算，直到误差小于预设值为止。经过几次迭代后，可以得到根号3的近似值。

例如，取初始值 x_0 = 1.5，则第一次迭代 x_1 = (1.5 + 3/1.5) / 2 = 1.75，第二次迭代 x_2 = (1.75 + 3/1.75) / 2 ≈ 1.7321，误差已经很小了。

需要注意的是，不同计算方法得到的近似值精度不同，需要根据实际应用需求选择合适的近似值。根据公开资料显示，采用不同算法，可以得到精度更高的近似值，例如1.732050807568877。

根号3的开方计算

虽然根号3无法精确表示，但我们可以利用计算器或计算机直接计算其数值。大多数计算器和计算机软件都内置了开方运算功能，直接输入3，再点击开方按钮即可得到根号3的近似值。

在没有计算器的情况下，可以使用查表法或者一些近似计算公式来估算根号3的值。一些数学工具书中会提供常见的无理数的近似值表格，可以方便地查找到根号3的近似值。

当然，还可以使用一些传统的开方计算方法，例如试商法等，但是这些方法计算过程较为繁琐，并且计算精度也相对较低，在实际应用中并不常用。

一些高级计算器和数学软件还可以提供根号3的精确表达式，虽然表达形式可能比较复杂，但是这些表达式在理论研究中具有重要意义。比如，在高等数学中，根号3常常作为一些公式中的常数出现。

根号3在数学中的应用

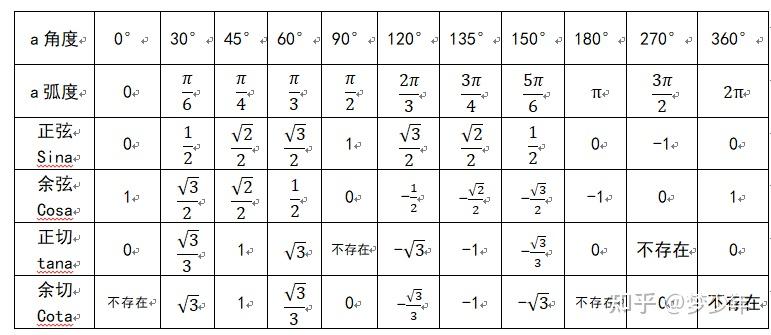
根号3在数学中广泛应用，它是许多数学公式和定理中的重要组成部分。例如，在三角函数中，正三角形的边长与高的关系就涉及到根号3。

在几何计算中，根号3也经常出现。例如，计算正三角形的面积、正六边形的边长等等，都需要用到根号3。

此外，在高等数学中，根号3也常常作为一些公式中的常数出现。例如，在计算积分、微分方程等问题时，根号3可能会出现在结果中。

在坐标系中，我们可以用根号3来表示一些特殊的向量或点的坐标。比如，在二维直角坐标系中，(1,√3)这个点与x轴正方向所成的夹角就是60度。

根据相关研究表明，根号3的数学特性使其在许多数学模型的构建中扮演着不可或缺的角色。

根号3在实际生活中的应用

• 在建筑工程中，根号3常常用于计算斜坡的坡度和长度，例如，设计屋顶坡度或计算桥梁的斜拉索长度。
• 在物理学中，根号3用于计算一些物理量，比如在力学中计算合力、在电学中计算阻抗等。
• 在电子工程中，根号3经常用于计算三相电路的参数。
• 根号3也出现在一些几何图形的设计中，例如在艺术设计中，一些具有对称性的图案的设计中就可能需要用到根号3。
• 在测量学中，根号3可以用于计算一些不规则形状的面积。例如，计算一些三角形的面积，就可能会用到根号3。

根号3的计算误差分析及未来发展

由于根号3是无理数，任何计算都存在一定的误差。误差的大小取决于计算方法和精度要求。

在实际应用中，需要根据精度要求选择合适的计算方法和近似值。例如，在工程计算中，需要保证计算结果的精度满足工程要求；而在一些科学计算中，则需要更高的计算精度。

随着计算机技术的发展，计算根号3的精度越来越高，未来可以使用更精确的算法和更强大的计算机来计算根号3，从而降低计算误差。

一些新的算法和方法也在不断被研究和开发，这些算法和方法可以有效地提高根号3的计算精度和效率。

权威机构指出，未来根号3的计算精度将不断提高，满足更精密的计算需求。