平均值怎么算？详解各种平均数的计算方法及应用场景

本文深入浅出地讲解了平均值怎么算，涵盖了算术平均数、加权平均数、几何平均数和调和平均数等多种计算方法，并分析了它们的优缺点及应用场景。文章还探讨了平均值在实际生活中的应用和未来发展趋势，旨在帮助读者更好地理解和应用平均值这一重要的统计指标，避免在运用平均值计算及分析过程中出现偏差和错误。

算术平均数：最常见的平均值计算方法

算术平均数，简称平均数，是最常见、最易理解的平均值计算方法。它通过将所有数值相加后除以数值的个数来计算。例如，计算5、10、15、20四个数字的平均数，则计算方法为：（5+10+15+20）/4 = 12.5。

算术平均数适用于大多数数据分布均匀的情况。例如，计算学生考试成绩的平均分、计算商品的平均价格等。但是，算术平均数容易受到极端值的影响。如果数据集中存在一些极端值（例如，一个人的收入远高于其他人），那么算术平均数就会偏高，无法真实反映数据的整体水平。

例如，某公司员工月收入分别为：3000元，3500元，4000元，4500元，100000元。算术平均数为：（3000+3500+4000+4500+100000）/5 = 22000元。这个平均数明显高于大多数员工的实际收入水平，这说明算术平均数受到了极端值的影响，无法真实反映该公司的员工收入水平。因此，在使用算术平均数时，需要考虑数据的分布情况，必要时需对极端值进行处理。

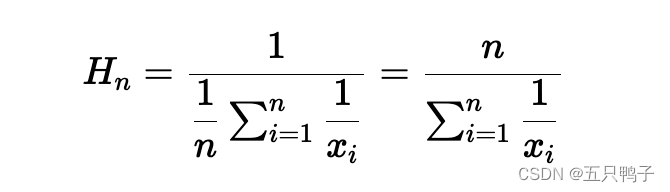
加权平均数：考虑权重的平均值计算

加权平均数是另一种常用的平均值计算方法，它考虑了每个数值的权重。权重是指每个数值对整体平均值的影响程度。加权平均数的计算方法是：将每个数值与其权重相乘，并将所有乘积相加，再除以所有权重的总和。

例如，某学生的期末成绩由平时成绩（权重40%）和期末考试成绩（权重60%）组成。平时成绩为85分，期末考试成绩为90分。则该学生的期末总成绩为：（85*0.4）+（90*0.6）= 87分。

加权平均数广泛应用于各种领域，例如：计算学生的GPA、计算投资组合的平均收益率、计算商品的加权平均成本等。与算术平均数相比，加权平均数更能反映不同数值的重要性，在实际应用中也更具有实用性。

在实际计算中，如果权重总和不为1，则需要先将权重进行标准化处理。比如，若某指标分别赋予权重为2，3，5，则在计算前需要将权重转换为：2/(2+3+5)=0.2，3/(2+3+5)=0.3，5/(2+3+5)=0.5。

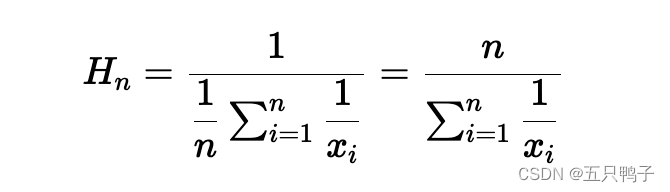
几何平均数与调和平均数：特殊场景下的平均值计算

除了算术平均数和加权平均数，还有几何平均数和调和平均数。几何平均数适用于计算比率或百分比的平均值，例如计算多年投资收益率的平均增长率。它的计算方法是将所有数值相乘，再开n次方（n为数值个数）。

例如，某股票三年收益率分别为10%、20%、30%，则三年平均增长率为：（1.1*1.2*1.3）^(1/3) -1 ≈ 19.1%。

调和平均数则适用于计算速率或比率的平均值，例如计算平均速度。它的计算方法是将所有数值的倒数相加，再取倒数。例如，某人往返一次，去程速度为60公里/小时，回程速度为40公里/小时，则平均速度为：2/(1/60+1/40) = 48公里/小时。

几何平均数和调和平均数在特定领域应用较多，例如经济学、金融学等，需要根据具体场景选择合适的平均数计算方法。

平均值的优缺点及潜在风险

• 平均值可以简化数据，方便理解和比较。
• 平均值可以反映数据的集中趋势，提供总体概况。
• 平均值计算方法简单，易于掌握和应用。
• 平均值容易受到极端值的影响，可能无法真实反映数据的实际情况。
• 平均值可能掩盖数据中的重要信息，导致误判。
• 使用平均值时需谨慎，需结合其他统计指标进行综合分析。
• 不同类型的平均值适用于不同的场景，需根据具体情况选择合适的平均值类型。
• 平均值不能反映数据的离散程度，需要结合方差、标准差等指标进行综合判断。
• 平均值计算结果容易被误解或滥用，需要清晰地表达计算方法和结果的含义。
• 平均值在社会经济领域常常被用来评价一个群体的整体水平，但其可能忽视群体内部的差异性和不平等现象。

平均值在实际生活中的应用及未来发展趋势

平均值在日常生活中应用广泛，从计算考试平均分到分析股票市场趋势，平均值都扮演着重要的角色。例如，政府部门使用平均值来计算居民收入、消费支出等宏观经济指标，企业则用平均值来衡量产品质量、员工绩效等。

随着大数据时代的到来，数据的规模和复杂性不断增加，传统的平均值计算方法面临着新的挑战。未来的平均值计算方法可能需要结合人工智能、机器学习等技术，以更好地处理海量数据，提取有价值的信息。同时，对平均值的解释和应用也需要更加谨慎和全面，避免误导和滥用。

例如，随着人工智能的应用，未来可能会出现更复杂的平均值计算方法，例如考虑数据权重、数据波动性等因素的加权平均值，或者根据不同的数据类型选择最优的平均值计算方法。这需要数学家、统计学家和计算机科学家等的共同努力。