本文详细讲解了平方根怎么算,从平方根的概念和基本计算方法开始,依次介绍了运用计算器计算平方根、手工开方计算方法以及平方根的实际应用,并探讨了其在不同领域中的应用以及未来的发展趋势,帮助读者全面掌握平方根的计算方法和应用技巧,例如学习如何用计算器快速计算平方根以及如何进行手工开方计算等。
平方根的概念及基本计算方法
平方根,简单来说,就是一个数的平方等于另一个数。例如,因为 2 的平方是 4,所以 4 的平方根是 2。但这只是最基本的概念,实际计算中,我们需要掌握不同的方法来求解平方根。
对于一些简单的数字,例如 4、9、16 等完全平方数,我们可以直接通过记忆或者简单的运算找到它们的平方根。比如,我们知道 9 的平方根是 3,因为 3*3=9。然而,对于大多数数字,直接找到精确的平方根就比较困难,需要借助一些计算技巧或工具。
历史上,人们很早就开始研究平方根的计算方法,例如古巴比伦人就发展出了一种高效的算法。现代数学中,我们则有更精确和快捷的计算方法,比如牛顿迭代法,这是一种数值逼近的方法,可以计算出任意精度下的平方根。此外,我们日常生活中,计算器也成为我们计算平方根最常用的工具。
了解了平方根的概念和基本计算后,我们就可以深入探讨不同类型的平方根计算方法了。
运用计算器计算平方根
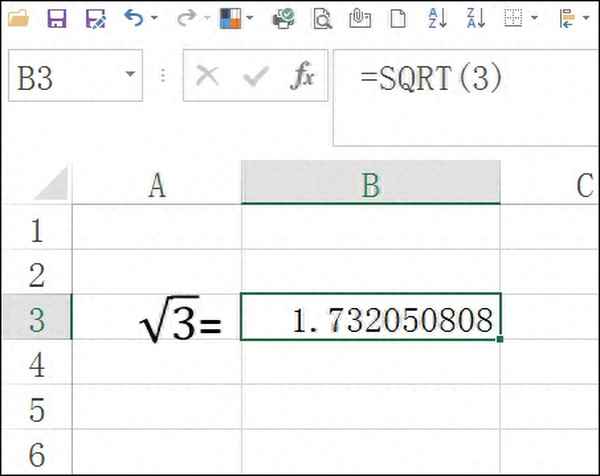
在日常生活中,计算器是计算平方根最便捷、高效的方式。几乎所有计算器都带有开平方根的按键,通常是一个带√符号的按键。只需要输入你需要计算的数字,然后按下开平方根按键,计算器就能立即显示出结果。
例如,计算 169 的平方根,你只需要在计算器中输入 169,然后按下开平方根按键,计算器就会显示结果为 13。需要注意的是,计算器计算的平方根通常为非负数(正数),即算术平方根。
此外,许多科学计算器还提供了更高级的计算功能,例如计算复数的平方根等等。但是,对于日常的计算,普通计算器已足够满足需求。熟练使用计算器,可以极大地提高我们计算平方根的效率。
计算器的普及大大降低了人们计算平方根的门槛,使得更多的人能够轻松运用平方根解决实际问题,其在科技、工程以及日常生活的应用也越来越广泛。

手工开方计算方法及其实际应用
虽然计算器已经非常普及,但是了解手工开方计算方法仍然具有重要意义。一方面,它可以帮助我们理解平方根的本质,另一方面,在一些特殊情况下,例如没有计算器或需要进行近似计算时,手工开方计算方法仍然非常实用。
传统的手工开方计算方法较为复杂,需要掌握一定的算法步骤,对于初学者来说,理解和掌握这些步骤可能需要一些时间和练习。通常来说,这类方法涉及到一系列的估算、试商和调整,最终逐步逼近精确值。历史上,许多数学家都对开方计算方法进行过研究和改进,使之更加简便易行。
除了传统的开方方法,还可以通过一些近似计算的方法,例如利用一些已知的平方数来进行估算,快速得到一个较为接近的近似平方根值。这在精度要求不高的情况下,可以大大简化计算过程,提高计算效率。
理解手工开方计算的步骤和技巧有助于加深我们对平方根运算的理解,并且可以在没有计算器等电子工具的情况下,也能完成对平方根的求解工作。
平方根的实际应用及未来发展趋势

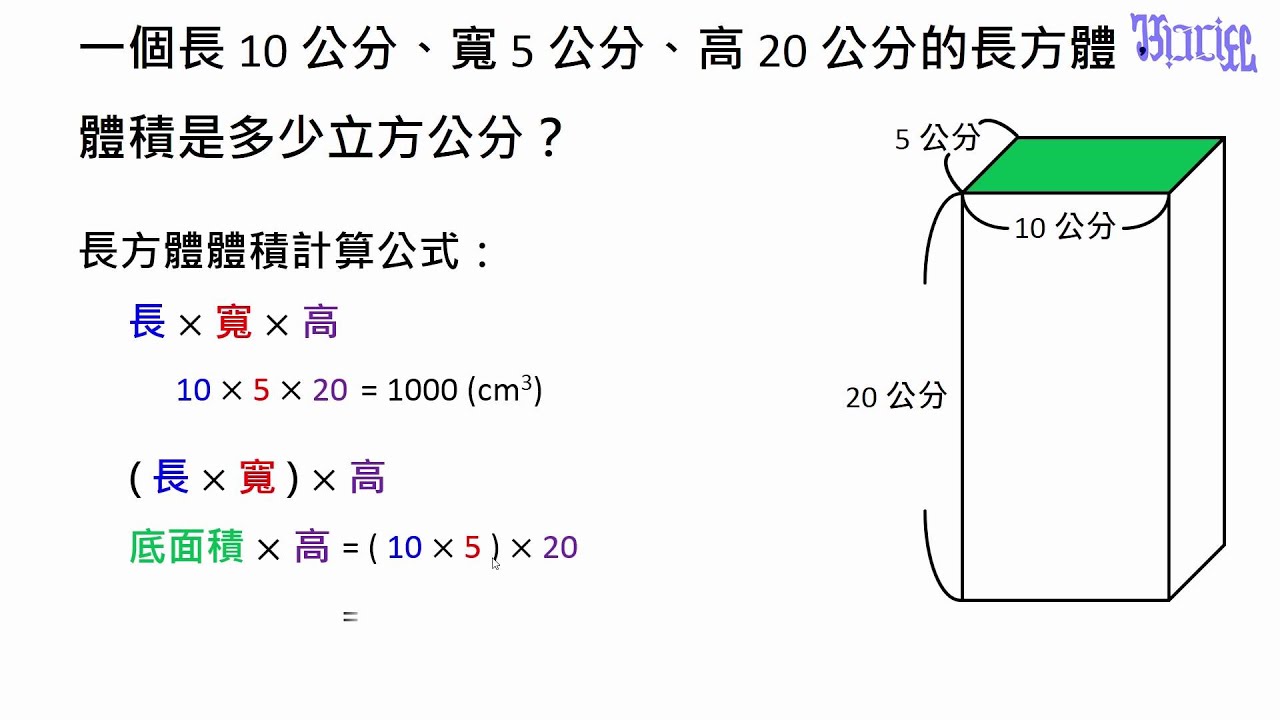
- 在几何学中,计算边长、面积、体积等常常需要用到平方根。例如,计算一个正方形的边长,只需将面积开平方即可。
- 在物理学中,许多公式中也包含平方根,例如计算速度、加速度、能量等。
- 在工程学中,平方根被广泛应用于结构设计、力学分析等领域。
- 在计算机科学中,平方根计算是许多算法的基础,例如图像处理、游戏开发等。
- 在金融领域,计算投资回报率等也会用到平方根。




 鄂ICP备15020274号-1
鄂ICP备15020274号-1