本文深入浅出地讲解了圆心角度数的计算方法,涵盖了多种计算公式和应用场景,并分析了误差控制和未来发展趋势。读者可以根据实际需要,选择合适的公式和方法来计算圆心角,并根据情况控制计算精度。文章还探讨了圆心角计算在工程、天文、地理等领域的应用,以及在复杂条件下的求解方法,希望能够帮助读者更好地理解和掌握圆心角的计算。
理解圆心角的概念及其与弧长、扇形面积的关系
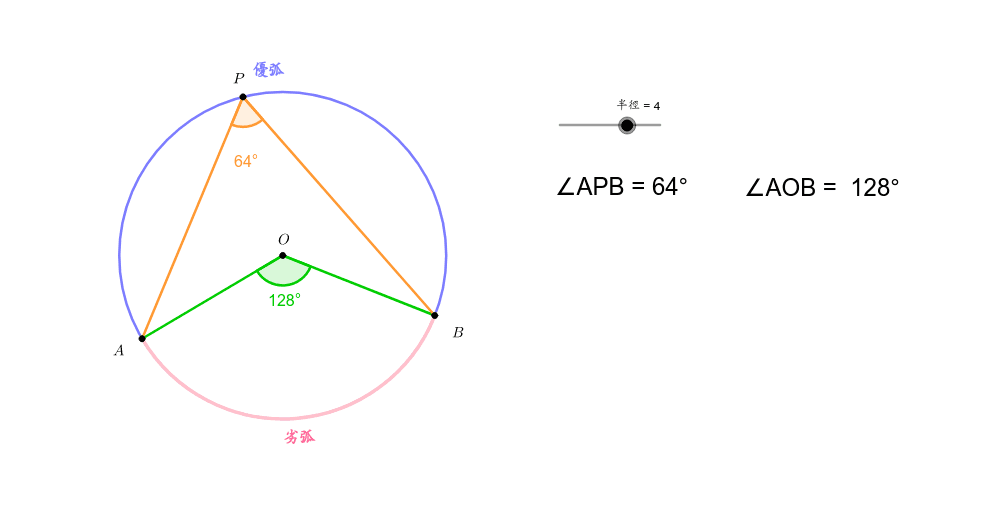
要计算圆心角度数,首先必须理解圆心角的概念。圆心角是指顶点在圆心的角,它的两条边都与圆相交。圆心角的大小直接与它所对的弧长和扇形面积相关。
已知圆的半径为r,弧长为l,则圆心角θ(以弧度制表示)的计算公式为:θ = l/r。如果需要得到角度数,则将弧度值乘以180/π即可。例如,一个圆的半径为5厘米,弧长为10厘米,那么圆心角为θ = 10/5 = 2弧度,换算成角度数为2 * 180/π ≈ 114.6度。
如果已知扇形面积S和半径r,则圆心角θ(以弧度制表示)的计算公式为:θ = 2S/r²。同样地,将弧度值乘以180/π即可得到角度数。比如,一个扇形的面积是20平方厘米,半径是4厘米,则圆心角为θ = 2*20/4² = 2.5弧度,约为143.2度。
理解这些基本公式是计算圆心角度数的关键第一步。在实际应用中,根据已知条件选择合适的公式进行计算即可。
不同条件下圆心角度数的求解方法
在实际问题中,我们可能面对各种不同的已知条件。除了上述已知弧长和半径、已知扇形面积和半径的情况,还可能遇到其他情况,例如:已知圆心角所对的弦长和半径。这时,我们需要利用三角函数知识进行求解。
假设圆的半径为r,弦长为c,圆心角为θ,我们可以通过余弦定理求解:c² = 2r²(1 - cosθ)。通过变形,我们可以得到cosθ = 1 - c²/2r²,进而求出θ。例如,如果半径为6厘米,弦长为8厘米,则cosθ = 1 - 8²/(2*6²)= 1/9, θ = arccos(1/9) ≈ 83.6度。
需要注意的是,在实际计算中,要根据具体问题选择合适的公式和方法。如果题目中只给出部分条件,可能需要结合其他的几何知识进行综合分析和求解。
圆心角度数计算在实际生活中的应用
- 地图投影和地理信息系统:精确的圆心角计算对于地图投影和地理信息系统的准确性至关重要。
- 机械设计:在齿轮设计、凸轮设计等机械设计领域,圆心角计算是进行精确计算的基础。
- 建筑工程:在建筑设计中,圆形建筑、拱形结构的设计都需要运用圆心角的知识。
- 天文观测:天文学中对于天体运行轨迹的计算,也离不开圆心角的计算。
- 钟表设计:钟表表盘的刻度设计,就需要精确的圆心角计算,以确保时间显示的准确性。
圆心角度数计算的误差分析与精度控制
在圆心角度数的计算过程中,由于测量误差、计算方法的局限性等原因,可能会出现一定的误差。因此,在实际应用中,需要重视误差分析,并采取措施来控制计算精度。
例如,在测量弧长或半径时,测量仪器的精度会直接影响计算结果的准确性。可以使用更高精度的仪器,或者进行多次测量取平均值,以减少测量误差。此外,选择合适的计算公式和方法,以及进行必要的误差修正,也能提高计算精度。
对于一些精度要求较高的场合,例如航天航空等领域,可能需要采用更精确的算法,或者结合其他测量手段,以保证计算结果的可靠性。
圆心角计算的未来发展趋势与挑战

随着科技的进步,圆心角计算方法也在不断发展和完善。例如,计算机技术的应用使得复杂的计算变得更加容易和快速。一些基于计算机辅助设计(CAD)的软件可以自动进行圆心角的计算,并提供更精确的结果。
未来,随着人工智能和机器学习技术的发展,可能会出现更加智能化的圆心角计算方法,能够自动识别和处理各种复杂的情况。
然而,圆心角计算也面临一些挑战,例如如何处理不规则形状的物体、如何提高计算精度和效率等。需要进一步研究和探索新的算法和方法,以应对这些挑战。






 鄂ICP备15020274号-1
鄂ICP备15020274号-1