本文详细阐述了已知正方形面积如何求边长,包括计算公式、步骤、实际应用及可能遇到的问题。文章以清晰的步骤讲解了开平方运算方法,并通过实际案例分析了正方形边长计算在土地规划、建筑工程和室内设计等领域的应用。此外,文章还探讨了计算精度、单位换算等问题,以及未来正方形面积与边长计算的发展趋势,如人工智能技术在几何计算中的应用。掌握正方形面积与边长计算,对于提升几何计算能力,解决实际问题至关重要。
正方形面积与边长的关系:公式及推导

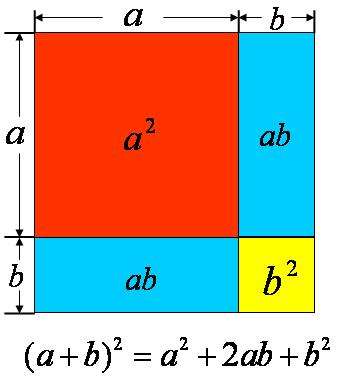
正方形,作为一种特殊的几何图形,其面积计算公式简洁明了:面积 = 边长 × 边长,或者用数学符号表示为 S = a² ,其中 S 代表面积,a 代表边长。
这个公式的推导基于正方形的定义:正方形具有四个相等边长和四个直角。我们可以将一个正方形分割成多个更小的正方形或者长方形,通过观察这些小图形的面积关系,推导出正方形的面积公式。
例如,一个边长为 2 厘米的正方形,可以分割成四个边长为 1 厘米的小正方形,每个小正方形面积为 1 平方厘米,因此总面积为 4 平方厘米。这与公式 S = a² (2²=4) 的结果一致。
在实际应用中,这个公式极其重要,广泛应用于建筑工程、土地测量、室内设计等各个领域。例如,建筑工程师需要根据地基的面积(正方形)计算所需材料的数量;室内设计师则根据房间面积来规划家具摆放。
理解正方形面积与边长的关系,是掌握平面几何的基础,也是解决更复杂几何问题的前提。
已知正方形面积求边长的计算步骤与方法
已知正方形的面积,求其边长,只需进行简单的开平方运算。假设正方形面积为 S,边长为 a,则计算公式为:a = √S。
具体的计算步骤如下:
1. 确认正方形的面积 S。
2. 使用计算器或手工计算求 S 的平方根。
例如,已知正方形面积为 16 平方厘米,则边长 a = √16 = 4 厘米。如果面积为 25平方米,则边长 a = √25 = 5 米。
需要注意的是,开平方运算结果可能为非整数,此时需要根据实际情况进行取整或保留小数位数。比如,一个正方形面积是 10平方厘米,那么它的边长是 √10 ≈ 3.16 厘米。这在实际应用中需要注意精度。
对于一些特殊的面积,例如完全平方数(例如 4,9,16,25等),可以直接根据平方根的知识快速得到结果。而对于非完全平方数的面积,需要使用计算器或公式进行计算。
熟练掌握开平方运算,可以高效地解决已知正方形面积求边长的计算问题。
已知正方形面积求边长的实际应用及案例分析
- 土地面积规划:在农村土地承包中,经常需要根据已知的土地面积计算土地的边长,从而进行合理的规划和利用。
- 建筑工程设计:建筑工程师根据地基面积(正方形)计算所需材料的数量,例如地砖、水泥等。
- 室内设计:室内设计师根据房间面积(正方形)设计家具摆放和空间布局。
- 包装设计:正方形包装盒的设计也需要根据产品体积(正方形)计算包装盒的边长。
- 艺术创作:在某些艺术创作中,例如绘画和雕塑,也需要根据作品的面积(正方形)确定作品的边长。
正方形边长计算中可能遇到的问题与挑战
在实际应用中,计算正方形边长可能会遇到一些问题和挑战。首先,计算精度的问题不容忽视。当面积不是完全平方数时,开平方运算的结果通常是一个无限不循环小数。在工程实际中,我们常常需要进行近似计算,并根据实际情况确定小数的保留位数,以保证计算结果的精度。
其次,单位换算也是一个容易出错的地方。在进行计算时,一定要注意面积单位和边长单位的一致性,例如将平方米换算成平方厘米,或者将厘米换算成米等。
最后,对于一些复杂的实际问题,正方形面积的计算可能需要结合其他的几何知识和计算方法。例如,在计算不规则图形面积时,有时需要将不规则图形分解成多个正方形或者长方形,再分别计算其面积,最后求和。
总结与展望:正方形面积与边长计算的未来发展
总而言之,已知正方形面积求边长是一个看似简单的计算问题,但其背后的数学原理和实际应用却十分广泛。随着科技的进步,各种计算工具的普及和计算方法的改进,正方形面积与边长计算的效率和精度都在不断提高。
未来,随着人工智能、大数据等技术的进一步发展,我们有望看到更加高效、智能化的正方形面积和边长计算方法。例如,利用图像识别技术,我们可以直接从图像中获取正方形的面积信息,并自动计算出它的边长。
此外,在更复杂的几何问题中,正方形面积与边长计算仍然扮演着重要的角色,这需要我们不断探索新的算法和计算方法。在未来的数学教学中,也应该更加注重培养学生的几何思维和空间想象能力,从而更好地解决实际问题。





 鄂ICP备15020274号-1
鄂ICP备15020274号-1