负次方计算简易控制：从基础到高级应用

本文系统解释了负次方的计算方法，从基础原理到中高数学应用，又给出了生活中的应用例子，并对计算中的问题和解决措施进行了分析，最后对负次方计算的将来发展趋势进行了预测，希望帮助多数读者熟知负次方的计算方法。

负次方的基础原理

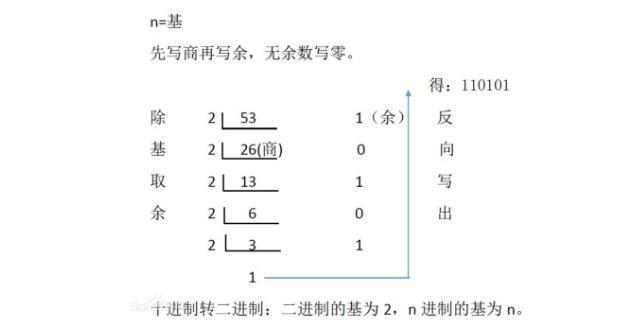
负次方的计算基于数学中的全部数学原理。它具体包括几个重要的方面。首先，一个数的负次方就是它的反数。例如，a^-1 = 1/a，这是很基本的知识。然后，按照这个原理，多次函数的负次方可以表现为其反数。例如，a^-2=1/a²， a^-n = 1/aⁿ，在这些计算中， a 不能为0。最后，应该注意到第一点。正数的负次方和负数的负次方的计算方法不同，需要特别注意。等于0的数的负次方是无定义的。

中高数学中负次方的应用

在中高数学中，负次方常用于解决多种问题，例如函数的反数运算、离数的计算等。负次方的计算在多项式中的应用也很常见，应用于分析多项式的问题，例如多项式的直线方程。在多项式的计算中，负次方的运算可以简化计算程序，使计算更加简单。再这些应用中，应该注意计算的精度。大多数情况下，需要用到高精度的计算方法才能保证计算的准确性。

生活中负次方的应用与例子

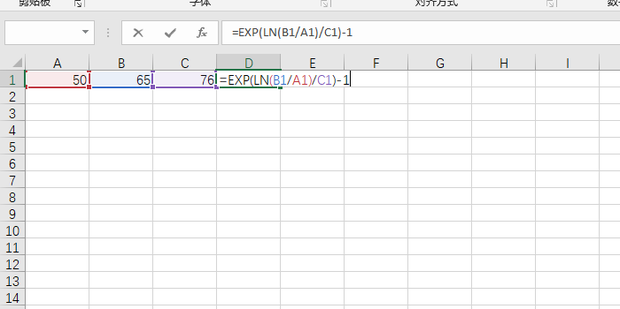
在生活中，负次方的应用很常见，例如计算某种物品的分量，如果一种物品的数量是 a，而每个分量的大小是1/a，那么就能够计算出有多少个分量。在经济中，负次方也常用于计算离数。例如某种资产的折旧率是 10%，那么这种资产在 n 年后的价值就是原价值的 (1-10%)ⁿ，如果 n 是负数，那么可以计算在几年前的价值。在生活中，负次方的应用还包括到离数、相似的等分量等多种情况。

负次方计算中的问题和措施

在负次方的计算中，常见的问题是多重运算的计算错误。为了防止这种错误，应该使用高精度的计算机或者软件进行计算。另一个问题是当基数为 0 时，负次方是无定义的。在实际计算中，应该注意到这个问题，防止计算出现错误。除此以外，对于一些复杂的负次方计算，可以使用相关的算法或者软件来进行计算，保证计算精度。在大量计算中，应该注意到数字精度的问题。

负次方计算的将来发展趋势

与数学其他领域的联系趋势一样，负次方的计算将会随着科技的发展而发展。在数学学科的推进下，更多新的计算方法和算法将会出现，使得负次方的计算更加简单、效率更高。随着计算机功能的提高，更多复杂的负次方计算将能够被解决。应该随着时间的推进，负次方的计算将会在多个领域得到更大的应用，也将会对我们的生活和工作带来更多的方便。