轻松掌握角平分线画法：几何作图技巧详解及应用

本文详细阐述了角平分线怎么画，从利用圆规和直尺作图的基本方法到角平分线的几何证明，以及在生活中的应用和未来发展趋势都做了深入浅出的讲解。文章还强调了避免作图错误的重要性，并通过具体的例子和实际应用场景帮助读者更好地理解和掌握角平分线的作图技巧和相关知识，例如用圆规画角平分线和角平分线在日常生活中的例子。

利用圆规和直尺作图：角平分线的标准画法

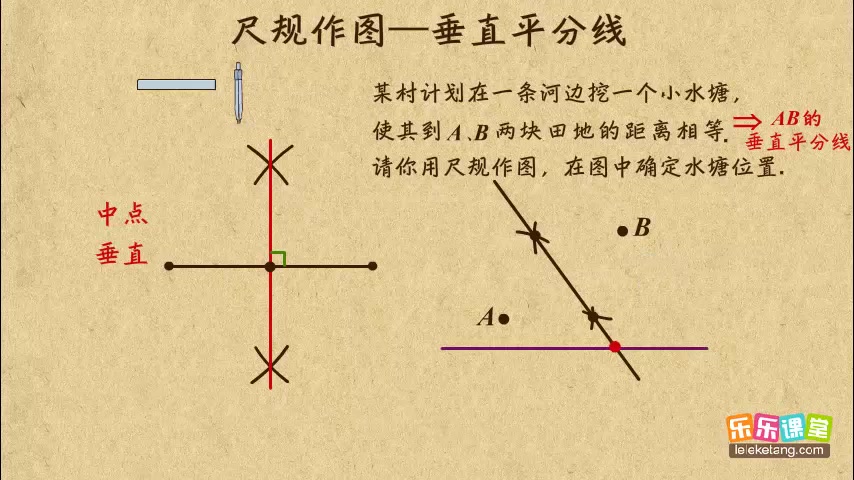
角平分线，顾名思义，是将一个角平分成的两条射线。那么，角平分线怎么画呢？最常用的方法是用圆规和直尺作图。首先，以角的顶点为圆心，任意画一个圆弧，与角的两边分别相交于两点。然后，分别以这两个交点为圆心，相同的半径画两个圆弧，使它们相交于一点。连接角的顶点和这个交点，这条线段就是角的平分线。

这个方法的原理在于，通过两次圆弧的作图，我们构造出了两个全等的三角形。这两个三角形的两条边分别与角的两边重合，而它们的第三条边相等。根据全等三角形的性质，我们可以证明连接角的顶点和两个圆弧交点的直线就是角的平分线。

例如，在学习三角形的内角平分线性质时，我们会频繁用到此方法。实践中，我们也可以用此方法平分一个任意角度的角，例如，在园林设计中，如果需要将一个角度为 120° 的道路分隔成两个 60° 的角度，就可以用这个方法精确地找到平分线。此外，在一些机械加工中，也需要用到角平分线来确保角度的精确性。

理解角平分线的几何证明：理论基础与应用

角平分线的作图方法虽然简单易懂，但其背后的几何原理却值得深入探讨。准确理解角平分线的几何证明，有助于我们更好地理解其本质，并能更熟练地运用相关定理解决几何问题。

许多几何题目的证明都依赖于角平分线的性质。例如，证明一个三角形的两条边相等，经常会用到角平分线上的点到角的两边的距离相等的性质。此外，在学习三角形全等或相似证明时，角平分线也扮演着重要的角色。理解角平分线的几何证明，可以帮助我们找到解题的关键点，避免陷入逻辑陷阱。

以等腰三角形为例，其顶角的平分线不仅平分顶角，也垂直平分底边。这个性质在很多几何题中都有体现，而且很多几何题目的解答都需要运用到这个性质。在解题时，如果能够熟练运用角平分线的性质，往往能够简化证明过程，提高解题效率。

避免常见错误：提高角平分线作图准确性

• 圆规半径不一致导致作图不准确
• 圆弧相交点不清晰影响精度
• 连接顶点和交点时出现偏差
• 忽略了圆弧与角的两边的交点，导致作图出错
• 没有仔细检查作图结果，导致结果不准确

角平分线在生活中的应用：从理论到实践

角平分线并非只存在于几何课本中，它在实际生活中也有着广泛的应用。例如，在建筑设计中，为了保证建筑物的美观和实用性，经常会用到角平分线来设计屋顶、窗户等结构。

在园林绿化中，角平分线也被广泛应用于道路规划、花坛设计等方面，以保证园林景观的协调性和美观性。此外，在一些机械加工中，角平分线也经常被用来精确控制角度，确保机械的正常运行。

例如，在裁剪衣服的过程中，经常需要将布料对折，并沿着对称轴裁剪，而这个对称轴其实就是布料角的平分线。再比如，在制作家具时，为了保证柜门的对称性，也需要使用角平分线的知识来保证柜门与柜体的精确拼接。这些生活中的例子都体现了角平分线的重要性。

角平分线作图的未来发展：技术与展望

随着科技的不断发展，角平分线的作图方法也可能会发生一些变化。例如，利用计算机辅助设计(CAD)软件，可以更加精确地绘制角平分线，并进行各种复杂的几何计算。

未来，角平分线在人工智能和虚拟现实等领域也可能会有新的应用。例如，在虚拟现实游戏中，可以利用角平分线的原理来设计更加逼真的场景和人物。

此外，随着人们对几何知识学习方式的不断改进，角平分线的教学方法也可能会更加多样化和直观化，让学生更好地理解和掌握这一几何概念。例如，引入交互式几何软件，可以让学生在互动中理解角平分线的概念及作图方法。