圆柱体的表面积怎么算？公式推导、应用案例及误区分析

本文系统讲解了圆柱体的表面积怎么算，从公式推导、应用案例到常见误区和未来发展趋势都进行了深入分析。文章强调了准确理解公式和避免计算错误的重要性，并结合实际案例阐述了圆柱体表面积计算在工程应用中的价值。掌握圆柱体表面积计算方法对于学习几何学和解决实际问题都具有重要意义，尤其对于圆柱体表面积计算公式及圆柱体表面积应用等长尾关键词的理解至关重要。

圆柱体表面积计算公式及推导

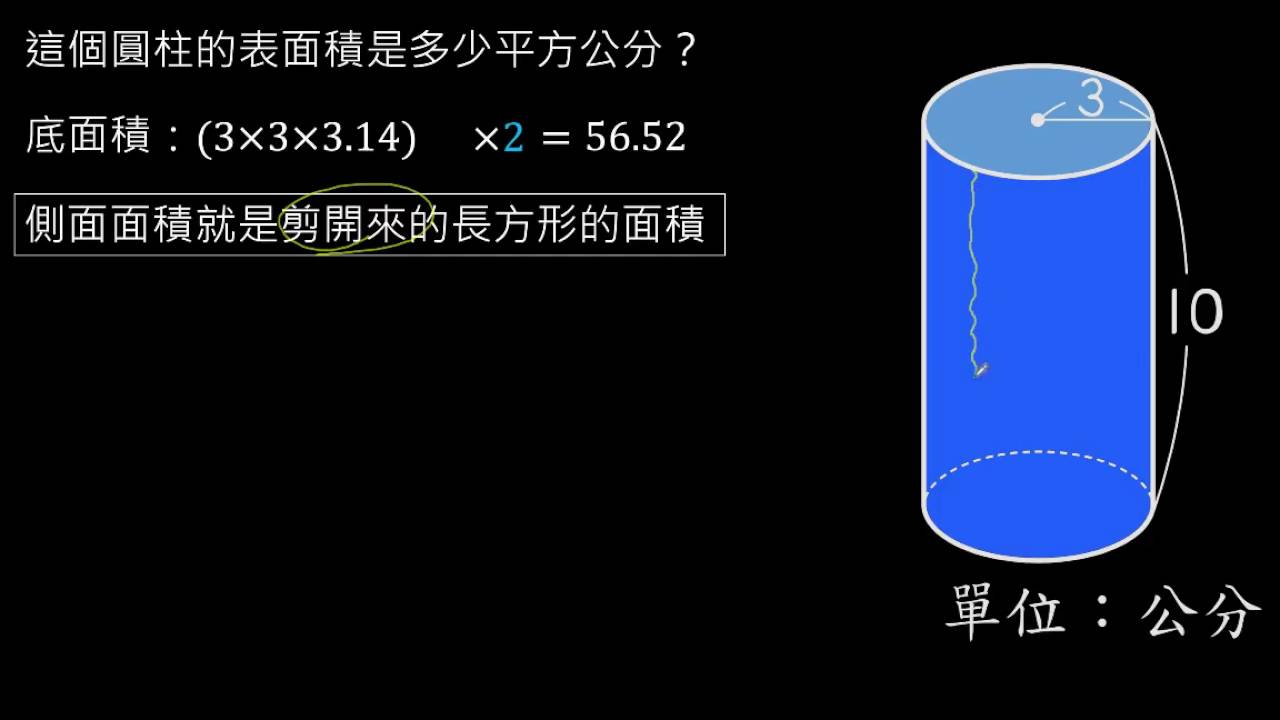
圆柱体的表面积计算是几何学中的一个基础问题，它指的是圆柱体所有表面积的总和。一个完整的圆柱体包含上下两个圆形底面和一个侧面。计算圆柱体表面积的关键在于理解其几何构成，并将其分解为易于计算的几何形状。

首先，我们来看圆柱体底面的面积。由于底面是圆形，其面积计算公式为：S底 = πr²，其中r代表圆柱体底面圆的半径。由于圆柱体有两个底面，因此两个底面的总面积为 2πr²。

接下来是圆柱体的侧面面积。如果将圆柱体的侧面展开，它会形成一个矩形。矩形的长等于圆柱体底面的周长(2πr)，宽等于圆柱体的高度(h)。因此，圆柱体的侧面面积为：S侧 = 2πrh。

最后，将底面面积和侧面面积相加，即可得到圆柱体的表面积：S表 = S底 + S侧 = 2πr² + 2πrh = 2πr(r + h)。

这个公式简洁明了，适用于各种类型的圆柱体。理解公式的推导过程，有助于更好地掌握计算方法，并能避免计算错误。例如，一个半径为5厘米，高为10厘米的圆柱体，其表面积为2π*5*(5+10) = 150π平方厘米。

不同类型圆柱体表面积计算的应用案例

实际应用中，圆柱体的形状并非总是标准的。例如，一些圆柱体可能具有倾斜的侧面，或者底面并非完美的圆形。这时，计算表面积的方法会稍微复杂一些，但基本原理仍然是将复杂的形状分解成简单的几何形状进行计算。

例如，一个具有倾斜侧面的圆柱体，可以将其侧面分解成若干个小的梯形，再计算每个梯形的面积，最后将所有梯形的面积加起来，即可得到侧面的总面积。底面的面积计算方法与标准圆柱体相同。

另一个例子是计算一个空心圆柱体的表面积。这时需要分别计算内外两个圆柱体的表面积，再将内外表面积相加，并减去重叠部分的面积，即可得到空心圆柱体的表面积。

在实际工程应用中，例如计算水塔、管道、烟囱等圆柱形结构的油漆用量或材料用量时，就需要运用圆柱体表面积计算公式。准确地计算表面积能有效地控制成本并避免材料浪费。一些复杂的工程结构可能需要借助计算机辅助设计软件进行更精确的计算。

圆柱体表面积计算中的常见误区及解决方法

• 忽略圆柱体的上下底面：一些同学在计算圆柱体表面积时，只计算侧面积，而忽略了上下两个底面的面积。
• 半径与直径混淆：在公式中，需要使用的是底面圆的半径(r)，而不是直径(2r)。
• 单位换算错误：在进行计算时，需要注意单位的一致性，例如半径和高度的单位必须相同，否则计算结果将会出错。
• 公式记忆错误：一些同学可能记错公式，例如将2πrh误记为πrh，从而导致计算结果出现偏差。
• 计算过程中的粗心大意：计算过程中，需要仔细检查每一个步骤，避免由于计算错误或粗心大意而导致最终结果出现错误。

圆柱体表面积计算的未来发展趋势与挑战

随着科技的发展，圆柱体表面积的计算方法也在不断发展和完善。计算机技术和人工智能技术的进步，使得我们可以对更复杂形状的圆柱体进行精确的表面积计算。例如，一些三维建模软件可以自动计算复杂几何形状的表面积，大大提高了计算效率和精度。

然而，随着计算精度要求的提高，也带来了一些新的挑战。例如，对于一些具有不规则形状的圆柱体，如何快速准确地进行表面积计算仍然是一个难题。此外，如何将圆柱体表面积计算与其他几何计算结合起来，以解决更复杂的工程问题，也是未来的研究方向。

未来的圆柱体表面积计算可能更加智能化，更加自动化，能够处理更复杂、更不规则的几何形状。这将对各个领域，例如建筑、工程、制造业等产生深远的影响。一些新的算法和模型的出现，将进一步提升计算效率和精度。