阴影部分的面积怎么求？详解各种图形阴影面积计算方法及技巧

本文深入探讨了阴影部分的面积怎么求，从基本方法到复杂图形的计算策略，并结合实际应用案例，全面讲解了各种计算方法及技巧，例如分割与组合法、坐标法，以及解决常见问题的方法。希望读者能够掌握这些方法，并在实际生活中灵活运用。掌握了不规则图形阴影面积计算和组合图形阴影面积计算方法，就能轻松应对各种阴影面积计算难题。

阴影面积计算的基本方法：分割与组合

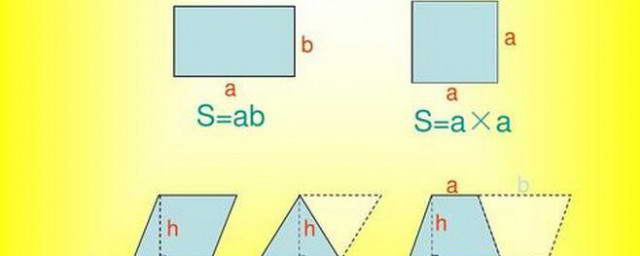
计算阴影部分的面积，最基本的方法是将复杂的阴影部分分割成若干个简单的几何图形，例如三角形、矩形、圆形或扇形等。

分割完成后，分别计算这些简单图形的面积，再将各个图形的面积相加，即可得到阴影部分的总面积。

例如，一个圆内有一个内接正方形，求阴影部分面积。我们可以将阴影部分分割成四个相同的弓形。先计算圆的面积，再计算正方形的面积，最后用圆的面积减去正方形的面积，再除以4即可得到一个弓形的面积，最后乘以4就是阴影部分面积。

这种方法尤其适用于不规则图形的阴影面积计算，通过巧妙的分割，将复杂的计算转化为简单的几何运算，大幅提高计算效率。

当然，并非所有阴影部分都能轻易地进行分割。有时，需要采用更巧妙的组合方式。例如，通过添加辅助线将阴影部分与已知图形结合，构成一个完整的几何图形，再利用整体与部分的关系求解阴影部分的面积。根据不同的图形和阴影的形状，我们可以灵活运用割补法、等积变换法等几何方法来简化计算。

常见平面图形阴影面积的求解

对于一些常见的平面图形，例如三角形、正方形、长方形、圆形等，其阴影部分面积的计算方法相对简单。

例如，在已知三角形的面积下，如果有一部分被遮挡，阴影部分的面积可以通过计算遮挡部分的面积，然后从总面积中减去即可。计算长方形阴影面积时，则通常先计算出阴影部分对应的长方形面积，或先求出被遮挡部分的面积再减去，方法很多，根据实际情况选择合适的方法。

需要注意的是，对于圆形和扇形的阴影部分面积计算，需要运用圆的面积公式和扇形的面积公式。如果阴影部分是圆环，则计算方法为大圆的面积减去小圆的面积；如果是扇形阴影，则需要先计算出扇形面积，再根据阴影部分的比例进行计算。

在计算过程中，需要根据图形的具体形状和位置进行调整，充分利用已知条件和几何知识，选择最简便的计算方法。不同的几何图形都有其独特的计算方式，学习和掌握这些基本图形的计算方法，是解题的关键。

复杂组合图形阴影面积的计算策略

• 合理分割图形，将复杂图形分解成多个简单的几何图形。
• 根据图形的特点，选择合适的辅助线，构造辅助图形。
• 运用几何变换，例如平移、旋转等，将图形转化成易于计算的形状。
• 熟练运用公式，准确计算各个简单图形的面积。
• 将各个简单图形的面积相加或相减，得到阴影部分的面积。

阴影面积计算中的常见问题及解决方法

在实际计算阴影面积的过程中，经常会遇到一些问题，例如：图形过于复杂、数据不足、计算过程繁琐等。

针对这些问题，我们可以采取一些解决方法。例如，对于复杂的图形，我们可以尝试采用坐标法来进行计算，将图形上的关键点用坐标表示出来，再根据坐标计算面积。

如果数据不足，则需要根据已知条件，运用相关的几何知识，推导出必要的参数。例如，通过三角函数或相似三角形等方法。

针对计算过程繁琐的问题，可以利用计算机辅助工具进行计算，提高计算效率。例如，可以使用几何画板等软件进行图形绘制和面积计算。

当然，解决问题的关键在于充分理解题目，并运用相应的数学知识和技巧，选择合适的计算方法。熟能生巧，多练习才能应对各种复杂的计算问题。

阴影面积计算在实际生活中的应用

阴影面积的计算方法不仅在数学学习中很重要，在实际生活中也有广泛的应用。例如，在建筑工程中，计算建筑物的阴影面积可以帮助我们更好地规划建筑物的位置和布局，避免阴影对建筑物内部采光的影响。

在园林设计中，计算阴影面积可以帮助我们更好地设计园林景观，例如，在设计花园时，可以根据阴影面积的大小来选择种植合适的植物。

在农业生产中，计算阴影面积可以帮助我们更好地安排农作物的种植位置，提高农作物的产量。

总之，阴影面积的计算方法在很多领域都有应用，掌握这种计算方法可以帮助我们解决许多实际问题。