本文详细阐述了梯形面积怎么求,从梯形面积计算公式的推导、不同类型梯形的面积计算、实际应用案例以及计算误区与技巧等方面进行了全面深入的分析。文章重点介绍了如何计算等腰梯形面积和直角梯形面积,并提供了多个生活中的实际应用案例,帮助读者更好地理解和掌握梯形面积的计算方法,避免常见的计算错误。
梯形面积公式推导与理解
梯形面积的计算是几何学中的一个基础问题,其公式的推导过程清晰明了,便于理解和记忆。我们可以将一个梯形分解成一个平行四边形和一个三角形,或者将两个相同的梯形拼成一个平行四边形来推导。
首先,我们考虑一个梯形,上底为a,下底为b,高为h。我们可以将该梯形沿对角线分成两个三角形。根据三角形的面积公式,第一个三角形的面积为(1/2)ah,第二个三角形的面积为(1/2)bh。将两个三角形的面积相加,得到梯形面积公式:S = (1/2)(a+b)h。
这个公式告诉我们,梯形的面积等于上底与下底之和的一半乘以高。公式简洁明了,便于记忆和应用。许多教材采用这种方法,直观易懂,有助于学生理解公式的来源和意义。
此外,我们还可以通过将两个全等的梯形拼成一个平行四边形来推导梯形面积公式。拼成的平行四边形的底边长度为a+b,高为h。平行四边形的面积为(a+b)h。由于两个梯形的面积相等,因此单个梯形的面积为(1/2)(a+b)h。这种方法同样简单易懂,且能直观地展现公式的几何意义。
理解公式推导过程对于灵活运用公式至关重要。例如,在实际应用中,我们需要根据题目的具体条件,选择合适的计算方法。
不同类型梯形的面积计算
掌握梯形面积计算公式后,我们还需要了解不同类型梯形的面积计算方法,例如等腰梯形、直角梯形等。
对于等腰梯形,其两腰长度相等,计算方法与普通梯形相同,只需根据题意求出上底、下底和高即可。例如,一个等腰梯形的上底为4cm,下底为10cm,高为6cm,则其面积为(1/2)(4+10)*6=42平方厘米。
直角梯形则有一角为直角,这使得我们可以更容易地求出其高。例如,一个直角梯形的两底分别为3cm和7cm,较短的腰为4cm。我们能发现这是一个直角梯形,高刚好是较短的腰长。因此,面积为(1/2)(3+7)*4=20平方厘米。在实际操作中,很多时候需要根据梯形的特性,巧妙地运用勾股定理等几何知识来辅助计算。
除了等腰梯形和直角梯形,还存在其他类型的梯形,但其面积计算方法基本一致,都是基于公式S = (1/2)(a+b)h。关键在于准确地识别梯形的几何特征,并根据题意求出上底、下底和高。
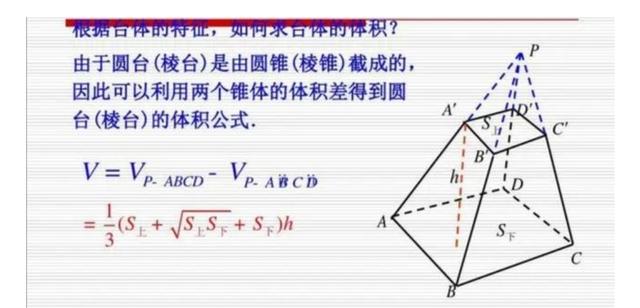
梯形面积计算在实际生活中的应用
- 测量土地面积:在农业、土地规划等领域,常常需要计算梯形的土地面积。
- 建筑工程:房屋、桥梁等建筑结构中,梯形结构也较为常见,计算面积对于工程设计和材料估算至关重要。
- 艺术设计:在绘画、设计等领域,梯形元素也经常出现,计算面积有助于设计布局和比例协调。
- 工程测量:在工程测量中,梯形面积计算可以应用于计算路面、水渠等工程的体积。
- 日常生活应用:如计算不规则形状花坛的面积,可将其近似为梯形进行计算。
梯形面积计算的误区及技巧
在梯形面积的计算中,也存在一些常见的误区和需要注意的技巧。
首先,要明确梯形上底、下底和高的含义,避免混淆。上底和下底是梯形的平行边,高是两平行边之间垂直距离。经常会出现学生误将斜边作为高的情况。
其次,要注意单位的统一。在进行计算时,要确保所有数据的单位一致,否则会造成计算结果的错误。例如,上底、下底的单位是米,高为厘米,则需要进行单位换算。
最后,可以根据题目的具体情况,选择合适的计算方法。如果梯形比较规则,可以直接运用公式计算;如果梯形比较复杂,则可以考虑将梯形分割成多个简单的图形,分别计算面积后再求和。
熟练掌握这些技巧,能够有效提高梯形面积计算的准确性和效率。例如,在面对复杂梯形时,分割成矩形和三角形的方法可以简化计算过程。
结语:梯形面积计算公式的推广与展望

梯形面积计算公式是一个简单而有效的几何公式,在数学学习和实际应用中都具有重要的作用。随着技术的不断发展,计算机和计算器等工具可以帮助我们更快速、更精确地计算梯形面积。
未来,随着对几何学研究的深入,可能会有更高级、更便捷的梯形面积计算方法出现。例如,利用更复杂的几何公式、数值方法或计算机辅助设计软件等。但无论计算方法如何发展,掌握基本公式和计算方法仍然是基础,是理解和应用更高阶方法的前提条件。
总而言之,理解并掌握梯形面积计算公式及相关知识,不仅能帮助我们解决数学问题,更能培养我们的逻辑思维能力和空间想象能力,在实际生活中发挥重要的作用。




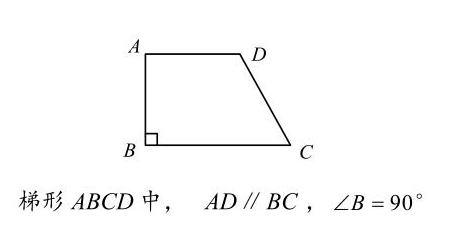
 鄂ICP备15020274号-1
鄂ICP备15020274号-1