本文详细讲解了平方面积计算公式、方法以及在实际应用中的案例分析,并分析了计算中可能存在的误差及应对策略。从长方形、正方形等规则图形到三角形、梯形等不规则图形,以及房屋面积计算、土地面积测量等实际应用,文章全面覆盖了平方面积计算的各个方面,旨在帮助读者掌握平方面积计算的技巧,并提高计算的精度和效率。文章还特别强调了单位统一的重要性以及各种误差的来源和规避方法,如测量误差和计算误差。
理解平方面积计算公式:基础篇
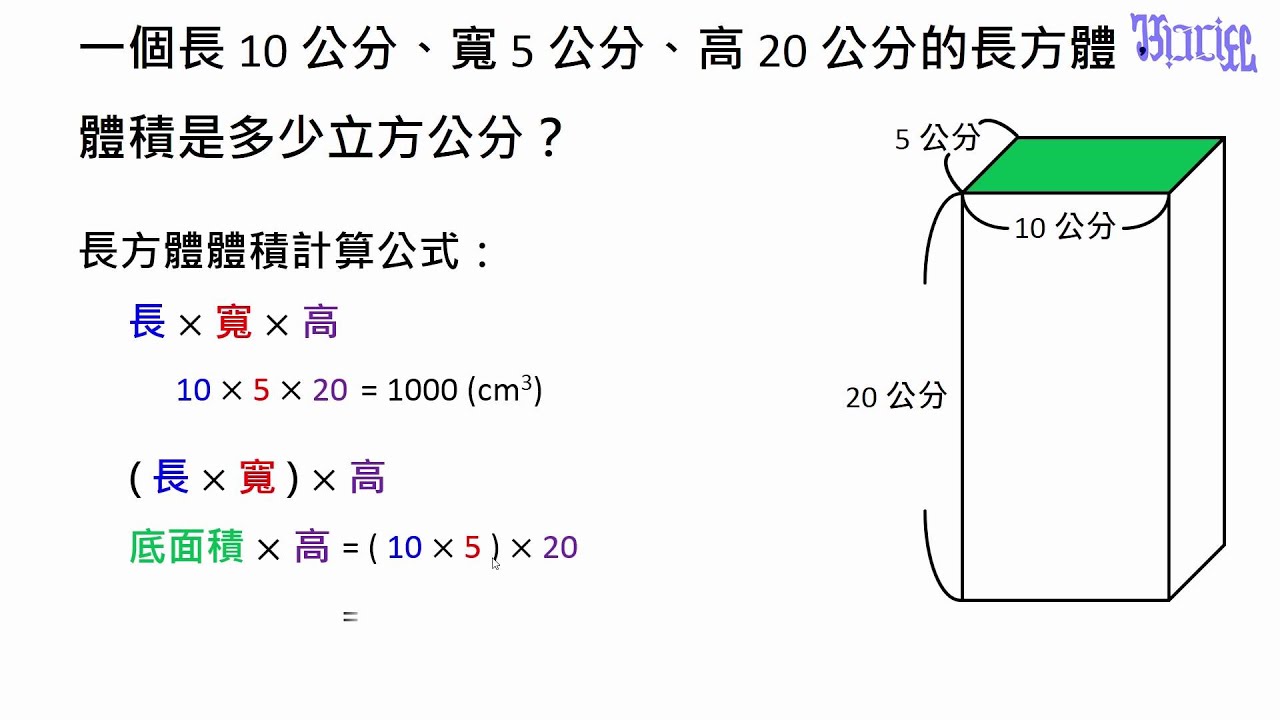
计算平方面积,最基础的公式莫过于长方形和正方形的面积计算:长方形面积=长×宽,正方形面积=边长×边长。这两个公式是所有平面图形面积计算的基础,理解透彻后,才能更好地理解更复杂的图形面积计算方法。
例如,一个长5米,宽3米的房间,其面积为5米×3米=15平方米。而一个边长为4米的正方形房间,其面积为4米×4米=16平方米。
掌握这两个基本公式后,可以轻松计算许多日常生活中常见的平面图形的面积,例如地板砖、地毯、桌面等等。许多其他的计算方法,都源于对这些基础公式的变形和组合。
值得注意的是,在进行面积计算时,一定要保证长度单位的一致性,否则计算结果将会出错。例如,如果长和宽的单位一个是米,一个是厘米,则需要先将单位进行统一,再进行计算。
三角形、梯形等不规则图形面积计算
除了长方形和正方形,生活中还会遇到各种不规则形状的平面图形,例如三角形、梯形、圆形等。这些图形的面积计算公式与长方形和正方形有所不同。
三角形的面积计算公式为:面积=(底×高)/2。其中,底是指三角形的底边长度,高是指三角形底边上的高。例如,一个底为6厘米,高为4厘米的三角形,其面积为:(6厘米×4厘米)/2=12平方厘米。
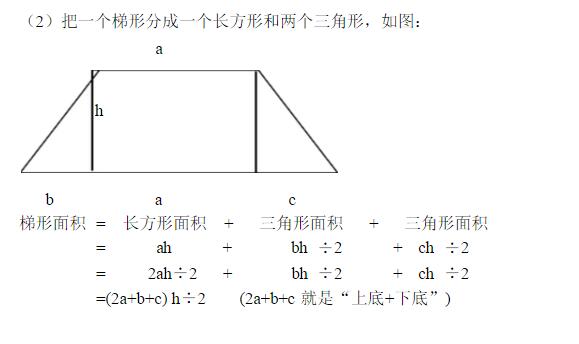
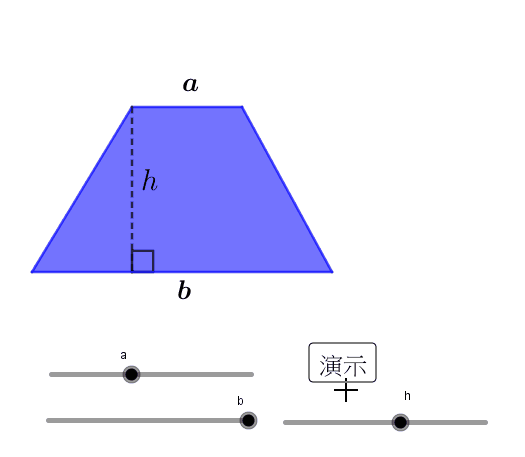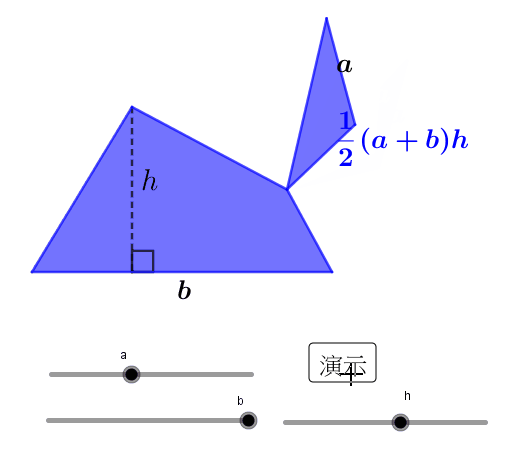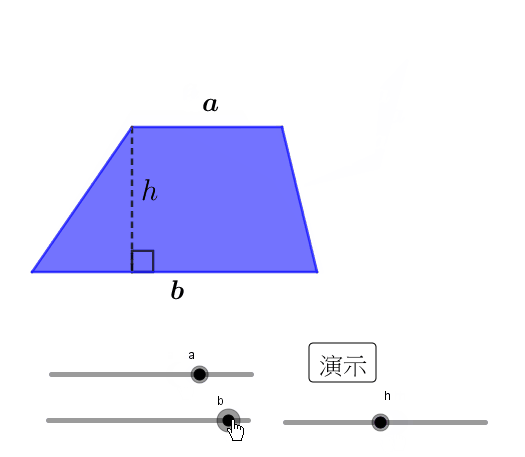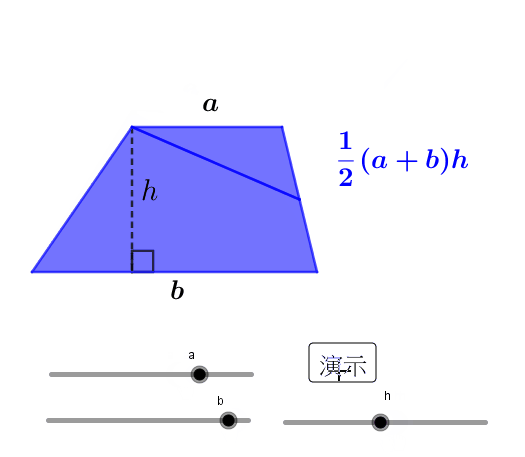
梯形的面积计算公式为:面积=(上底+下底)×高/2。其中,上底和下底分别指梯形的上下两条平行边的长度,高是指两条平行边之间的垂直距离。例如,一个上底为5米,下底为7米,高为3米的梯形,其面积为:(5米+7米)×3米/2=18平方米。
对于圆形,其面积计算公式为:面积=πr²,其中r为圆的半径。π约等于3.14159。
在实际应用中,有时需要将不规则图形分解成若干个规则图形,然后分别计算每个规则图形的面积,再将这些面积相加,即可得到不规则图形的总面积。
实际应用中的平方面积计算:案例分析
平方面积的计算广泛应用于各个领域,例如房屋面积计算、土地面积测量、工程设计等。
例如,在房屋买卖中,房屋面积是重要的参考指标,需要准确计算。通常情况下,房屋面积的计算会根据房屋的平面图进行,将房屋分解成若干个规则图形,然后分别计算面积,再相加即可得到房屋的总面积。需要注意的是,房屋面积的计算需要按照国家相关的规范进行,以确保计算结果的准确性。
在土地面积测量中,通常会使用专业的测量仪器,例如全站仪、GPS等进行测量。测量完成后,根据测量数据,可以计算出土地的面积。土地面积的测量需要考虑地形地貌等因素,以保证测量的精度。
在工程设计中,平方面积的计算也至关重要,例如道路设计、桥梁设计等,都需要进行精确的面积计算,以保证工程的质量和安全。
准确的平方面积计算对各种工程项目的成本控制至关重要。例如,铺设地板或瓷砖的工程,面积计算的精确性直接影响到材料用量的多少,从而影响工程的最终成本。
平方面积计算的误差分析及应对策略
在实际应用中,平方面积的计算难免会存在一些误差。这些误差可能来自测量误差、计算误差或其他因素。
测量误差是由于测量工具的精度限制或人为因素造成的。例如,使用卷尺进行测量时,由于拉力不均匀或读数错误,可能会导致测量误差。
计算误差是由于计算过程中的近似计算或四舍五入等操作造成的。例如,在计算圆形面积时,使用π的近似值会造成一定的计算误差。
为了减少误差,需要选择精度更高的测量工具,并严格按照计算公式进行计算。同时,也需要对计算结果进行必要的校验,以确保计算结果的准确性。
此外,对于一些形状复杂的图形,可以考虑采用数值计算方法或计算机辅助设计软件进行面积计算,以提高计算精度并减少人为误差。
在实际工作中,要重视测量与计算的规范性,并严格控制各种可能的误差源,最终提升计算结果的可信度。




 鄂ICP备15020274号-1
鄂ICP备15020274号-1