本文详细解释了如何理解“奇变偶不变符号看象限”,从奇偶函数的概念入手,深入探讨了象限变化与符号的对应关系,并结合函数图像绘制和实际应用,全面阐述了该方法的优缺点以及在不同场景下的适用性。文章还强调了结合其他分析方法进行更深入的理解,并展望了该方法未来的发展趋势。掌握“奇变偶不变符号看象限”以及相关的函数图像分析技巧,对学习和掌握数学知识至关重要。
理解“奇函数与偶函数”的概念
要理解"奇变偶不变符号看象限怎么理解",首先必须明确奇函数和偶函数的概念。奇函数是指满足f(-x) = -f(x)的函数,其图像关于原点对称;偶函数是指满足f(-x) = f(x)的函数,其图像关于y轴对称。例如,f(x) = x³ 是奇函数,因为(-x)³ = -x³ = -f(x);而f(x) = x² 是偶函数,因为(-x)² = x² = f(x)。理解这两个基本概念是后续理解象限变化的关键。
许多初学者容易混淆奇函数和偶函数的概念,常常将图像关于x轴对称误认为是偶函数。需要强调的是,图像关于x轴对称不属于奇函数或偶函数的定义。
在实际应用中,我们可以通过函数图像的特性来快速判断函数的奇偶性。例如,正弦函数sin(x)是奇函数,其图像关于原点对称;余弦函数cos(x)是偶函数,其图像关于y轴对称。掌握这些基本函数的奇偶性,可以帮助我们更好地理解和应用“奇变偶不变符号看象限”的规则。
象限变化与符号的对应关系
理解了奇偶函数的概念后,我们就可以探讨象限变化与符号的关系。“奇变偶不变,符号看象限”描述了奇函数和偶函数在不同象限的图像变化规律。对于奇函数,当x取负值时,函数值f(x)的符号与x的符号相反;对于偶函数,无论x取何值,函数值f(x)的符号总是与f(x)在第一象限的符号相同。
例如,对于奇函数f(x) = x³,在第一象限(x>0, y>0),f(x) > 0;在第二象限(x<0, y>0),f(x) < 0;在第三象限(x<0, y<0),f(x) > 0;在第四象限(x>0, y<0),f(x) < 0。这体现了“奇变”的特性,即函数值符号随着x的符号变化而变化。
对于偶函数f(x) = x²,无论x位于哪个象限,f(x)总是大于或等于0。这体现了“偶不变”的特性,即函数值的符号保持不变。这便是“奇变偶不变符号看象限”的直观体现。
利用“奇变偶不变符号看象限”快速绘制函数图像
- 快速判断函数的奇偶性,确定其图像的对称性
- 根据奇偶性判断函数在不同象限的符号
- 利用函数的特殊点(例如:零点、极值点)辅助作图
- 结合函数的周期性(对于周期函数)辅助作图
- 运用“奇变偶不变符号看象限”的规则,快速绘制函数草图
- 根据草图,结合函数的具体表达式,精细绘制函数图像
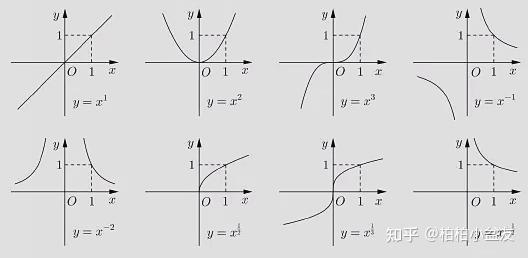
深入理解:超越简单的符号变化
虽然“奇变偶不变符号看象限”提供了一种快速判断函数图像在不同象限符号变化的便捷方法,但这仅仅是图像性质的一部分,而非全部。更深入的理解需要结合函数的导数、极值、渐近线等信息。
例如,即使知道了函数的奇偶性,也不能完全确定函数图像的具体形状。我们需要结合函数的单调性、凹凸性等信息来更准确地绘制图像。仅凭奇偶性判断图像在象限中的正负,可能会忽略一些重要的细节,例如函数图像可能在象限内出现拐点或波动。因此,在实际应用中,我们应该将“奇变偶不变符号看象限”与其他分析方法相结合,才能更全面地理解函数图像的性质。
此外,还有一些函数既不是奇函数也不是偶函数,例如f(x) = x + x²,对于这类函数,我们就需要采取其他的方法来分析其图像性质。
在实际应用中的局限性及拓展
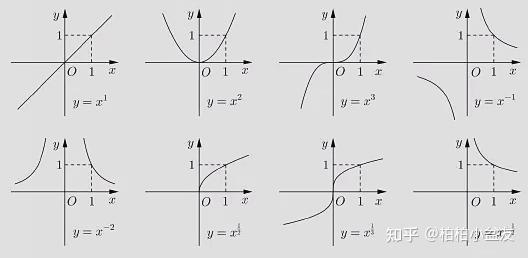
“奇变偶不变符号看象限”主要适用于初等函数图像的快速分析和绘制,对于一些较为复杂的函数,例如超越函数或分段函数,其适用性会受到限制。在这些情况下,需要结合更高级的数学工具和方法进行分析。
例如,对于一些复杂的超越函数,我们可能需要利用计算机软件进行数值计算和图像绘制,才能获得其图像的准确信息。
然而,“奇变偶不变符号看象限”作为一种基本的数学技巧,仍然在很多领域中发挥着重要的作用,尤其是在初等数学和理工科相关专业的学习中,它能够帮助学生快速理解和掌握函数图像的性质。未来,随着数学工具和计算方法的不断发展,该方法可能会与其他更高级的分析方法相结合,形成更加强大的函数图像分析体系。




 鄂ICP备15020274号-1
鄂ICP备15020274号-1