直角三角形的面积怎么算？详解公式、推导及应用场景

本文深入探讨了直角三角形的面积计算方法，从公式推导到实际应用，并分析了不同情况下的处理方法以及未来的发展趋势。学习如何计算直角三角形的面积不仅能帮助解决几何问题，还能在工程测量和建筑设计等领域发挥重要作用。掌握直角三角形面积计算技巧和直角三角形特殊情况处理方法，对于提升数学能力具有重要意义。

直角三角形面积计算公式及推导

直角三角形的面积计算是几何学中的基础知识，其核心公式简洁明了：面积 = (底 * 高) / 2。

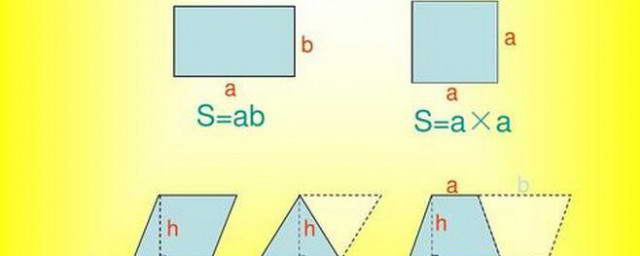
这个公式的推导过程可以基于矩形面积的理解。我们可以将一个直角三角形与其镜像组合成一个矩形。矩形的面积等于底乘以高，而直角三角形的面积恰好是这个矩形面积的一半。

例如，一个直角三角形的底为6厘米，高为8厘米，那么它的面积就是 (6 * 8) / 2 = 24平方厘米。这是一个非常直观的计算方法，即使是小学阶段的学生也能够轻松掌握。

理解这个公式推导的关键在于，将一个看似复杂的几何图形转化为我们更熟悉的简单图形，从而运用已知的知识解决问题。这体现了一种化繁为简的数学思想，在解决其他几何问题时同样适用。

不同类型直角三角形面积计算的应用场景

直角三角形面积计算的应用范围非常广泛，从简单的几何题到复杂的工程设计，都能看到它的身影。

在工程测量中，常需要计算土地面积或建筑物占地面积。如果地块形状是直角三角形，那么可以直接运用公式计算其面积。例如，规划一块直角三角形形状的绿地，需要知道其面积来确定种植树木的数量和所需材料。

在建筑设计中，直角三角形的面积计算也至关重要。例如，计算房屋的屋顶面积、墙面面积等等，这些都需要精确的面积计算，以确保材料用量的准确性和工程的顺利进行。这体现了数学在实际生活中的实用价值。

此外，在计算机图形学中，直角三角形也是最基本的几何单元之一，许多图形的绘制和计算都依赖于直角三角形的面积计算。 这表明了直角三角形面积计算的重要性， 甚至延伸到了计算机技术领域。

直角三角形面积计算中可能遇到的特殊情况及处理方法

• 当直角三角形的两条直角边长度已知时，直接套用公式即可。
• 如果已知斜边和一条直角边，则需运用勾股定理先计算出另一条直角边，再代入面积公式。
• 如果已知斜边和一个角，则需运用三角函数计算出两条直角边，再代入面积公式。
• 如果直角三角形是等腰直角三角形，则只需要知道一条直角边的长度，就可以计算出面积。
• 在实际应用中，可能需要考虑精度问题，运用更精确的测量工具和计算方法，以获得更准确的面积结果。

直角三角形面积计算的未来发展趋势及潜在挑战

随着科技的进步，直角三角形面积的计算方法也在不断发展和完善。未来，可能会出现更多更便捷的计算工具和方法，例如利用人工智能技术进行更快速、更准确的面积计算。

然而，在实际应用中仍然存在一些挑战，例如：对于形状不规则的近似直角三角形，如何更精确地计算面积？如何处理测量误差对计算结果的影响？如何结合新的技术手段，例如三维激光扫描技术，来提高测量精度和计算效率？这些都是未来需要研究和解决的问题。

此外，在教学中，如何更好地引导学生理解直角三角形面积计算公式的推导过程，以及公式在实际生活中的应用，也是一个需要关注的问题。

总而言之，直角三角形面积计算看似简单，但背后蕴藏着丰富的数学思想和应用价值，值得我们不断探索和研究。