扇形的面积怎么算？公式推导、应用及误区分析

本文深入浅出地讲解了扇形的面积怎么算，从公式推导、实际应用、常见误区以及未来发展趋势等多个角度进行了全面的分析。文中结合实际案例和数据，并对扇形面积计算的公式推导和弧度制的使用进行了详细的阐述，帮助读者更透彻地理解扇形面积计算方法，避免常见的错误，并对扇形面积计算的应用前景进行了展望。

扇形面积计算公式的推导与理解

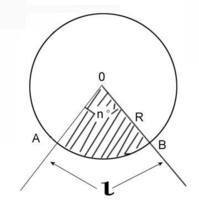
扇形的面积计算是平面几何中的一个基本问题，其公式的推导基于圆的面积计算。我们知道，圆的面积公式是πr²，其中r代表圆的半径。扇形可以看作是圆的一部分，它是由圆心和圆周上两点构成的。如果我们知道扇形的圆心角θ（以弧度为单位）和半径r，那么扇形的面积S就可以表示为：S = (θ/2π) * πr² = (1/2)θr²。

这个公式的推导过程其实很简单：一个圆的面积是πr²，而扇形所占圆的比例是θ/2π（θ是圆心角，以弧度为单位），因此扇形的面积就是圆面积的(θ/2π)倍。

理解这个公式的关键在于理解弧度制。弧度制是另一种度量角度的方式，它将角度与圆的半径联系起来。一个完整的圆周角是2π弧度，而扇形的圆心角θ则用弧度表示扇形所对的圆弧长度与半径的比值。

例如，一个半径为5厘米，圆心角为π/2弧度的扇形，其面积为：(1/2) * (π/2) * 5² = 25π/4 平方厘米。如果圆心角是用角度制表示，例如60°，则需要先将角度制转换为弧度制：60° = 60 * (π/180) = π/3弧度，然后代入公式计算。

一些初学者可能会混淆扇形面积公式和三角形面积公式，两者虽然都涉及到角度和长度，但计算对象和方法完全不同。务必理解公式的推导过程，才能避免混淆，正确运用。

扇形面积计算在实际生活中的应用

扇形面积的计算并非仅仅是数学课本上的理论知识，它在实际生活中有着广泛的应用。例如，在工程设计中，计算圆形部件的切割面积，或者设计钟表表盘时计算每个时间刻度的面积，都需要用到扇形面积计算公式。

在农业生产中，如果需要计算灌溉区域的面积，而灌溉区域是圆形的一部分，则也可以利用扇形面积计算公式来进行计算。

再比如，在园林设计中，常常会用到各种形状的花坛，如果花坛设计成扇形，那么在计算花坛面积时，就需要用到扇形面积的计算公式。设计过程中，计算花坛所占面积，便于进行材料的预估和成本的控制。

此外，在艺术设计领域，诸如蛋糕装饰、设计图案，甚至时装设计等，也常常会用到扇形。计算扇形面积可以帮助设计师更精准的控制设计元素，使作品更具美感和实用性。

从以上例子可见，扇形面积计算的应用范围很广，是一个实用性很强的数学知识点。理解并掌握扇形面积的计算，对于解决实际问题至关重要。

扇形面积计算中的常见误区与防范措施

在学习和应用扇形面积计算公式的过程中，一些常见的误区需要我们特别注意。首先，单位的换算问题，一些同学在计算过程中，容易混淆角度制和弧度制，导致计算结果出现错误。因此，在进行扇形面积计算时，必须先将角度制转换成弧度制，再代入公式进行计算。

其次，公式的记忆与理解。一些学生死记硬背公式，而忽略了公式的推导过程和内在的逻辑关系，这样容易造成对公式的理解不深，在应用过程中出现偏差。理解公式推导过程有助于加深对公式的理解，避免记忆错误。

最后，容易混淆扇形面积和其它相关图形面积，例如三角形、弓形等。在计算不同图形面积时，应根据图形的特征选择对应的计算公式。例如在计算弓形面积时，常常需要先求出扇形面积以及三角形面积，然后才能计算出弓形的面积。

为了避免这些误区，我们应该注重公式的理解和推导，熟练掌握角度制和弧度制的换算，并多做练习来巩固所学知识。在实际应用中，仔细审题，明确图形的特征，选择合适的计算公式，逐步计算，并注意单位的统一。

扇形面积计算公式的拓展与应用展望

• 在高等数学中，扇形面积的概念可以拓展到更复杂的几何形状的面积计算，比如曲边扇形的面积计算。
• 随着计算机技术的进步，利用计算机软件可以更快速准确的计算任意角度和半径的扇形面积。
• 在未来的教学中，可以结合多媒体技术，更直观地演示扇形面积计算公式的推导过程。
• 未来可以开发更多针对扇形面积计算的应用软件，方便用户进行计算，减少错误。
• 在人工智能领域，可以利用机器学习技术来进行扇形面积计算的优化和改进，提高计算效率和精度。