三角形面积计算方法详细解释：完全掌握各种情况下的计算技巧

闲云野鹤 2025-01-01 实时热搜 834 次浏览 0个评论

本文详细解释了三角形面积的基本公式及在平行、立和不平行三角形中的应用，并讨论了其在实际生活中的应用和未来发展前景。如何求三角形面积在建筑和农业中的应用很广，未来与大数据的结合也会更加精确。

三角形面积基本公式及定义

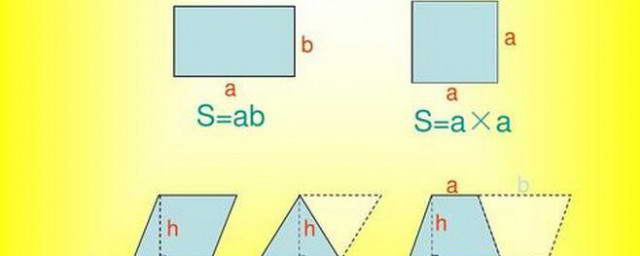
三角形的面积计算是基本的工程数学问题，它的基本公式是：面积 = (1/2) × 基线长×高度。这里的“基线长”指的是三角形的一边的长度，而“高度”指的是从对基线的顶点到对基线的对角的距离。对于平行三角形，这个公式直接可用；为了够完全理解，我们可以将三角形视为一个圆的一半大小，这样就很容易理解了。例如，一个平行三角形，基线长为 6兆米，高度为 4兆米，则其面积为 (1/2) × 6兆米 × 4兆米 = 12兆米²。

多种情况下的三角形面积计算

平行三角形： 直接使用基本公式，面积 = (1/2) × 基线长×高度。
立三角形：立三角形可视为两个平行三角形的和，将两个平行三角形的面积求出并相加，就可以求出立三角形的面积。
不平行三角形：为了求出不平行三角形的面积，可以将不平行三角形分解为多个平行三角形或者用分断法。
利用「定分法」：使用矢量的方法计算三角形的面积。这方法对于某些复杂三角形更为简单。
利用等高式：为了求出不平行三角形的面积，可以将三角形分解为两个平行三角形。这种方法对于一些特殊的三角形很有效。

三角形面积计算在实际生活中的应用

三角形面积的计算在生活中应用很广，从简单的地皮面积计算到复杂的工程设计，都需要使用三角形的面积计算。例如，在农业中，定量的粮米土地的面积计算就常用到三角形的面积计算方法；在建筑业中，建筑外墙的面积计算也常用到三角形的面积计算方法。有些工程项目具体情况很复杂，我们可以利用计算软件或者等工具来完成面积计算。并且，在数学研究中，对三角形面积的研究也是一个重要问题。