圆的面积怎么求？公式推导、实际应用及常见问题解答

本文详细阐述了圆的面积计算公式πr²，并从公式推导、不同形状圆形面积计算、实际应用和可能遇到的问题等多个角度进行深入分析，探讨了圆的面积计算在日常生活、工程技术等领域的广泛应用以及未来的发展趋势，例如人工智能技术在圆面积计算中的应用。文章还涵盖了圆形面积计算公式、不同形状圆形面积计算、不规则圆形面积计算等长尾关键词，旨在帮助读者全面、深入地理解和掌握圆的面积计算方法。

圆的面积计算公式：πr² 的前世今生

圆的面积计算公式，πr²，是几何学中最基础也是最重要的公式之一。它简洁优雅，却蕴含着深刻的数学思想。

理解这个公式的关键在于理解π（π约等于3.14159）和r（圆的半径）。π是一个无理数，代表圆周长与直径的比值，它是一个常数，无论圆的大小如何，这个比值都是不变的。而r则代表圆心到圆周上任意一点的距离。

那么，公式是如何推导出来的呢？一种常用的方法是利用微积分。将圆分割成无数个无限小的扇形，然后将这些扇形排列成一个近似的长方形，通过计算长方形的面积，就可以推导出圆的面积公式。当然，还有其他的推导方法，例如利用古希腊数学家阿基米德的穷竭法，也可以得到同样的结果。

这个公式的应用范围非常广泛，从日常生活中的计算，例如计算饼干、盘子、车轮的面积，到工程技术领域的计算，例如计算管道、水库、储油罐的容积，都有着极其重要的作用。掌握这个公式，不仅可以解决很多实际问题，更可以提升我们对数学的理解和应用能力。

历史上，许多数学家都为圆面积的计算做出了贡献，例如祖冲之精确计算了π的值，为圆面积的计算提供了更精确的基础。

不同形状圆形面积的计算方法：规则与不规则

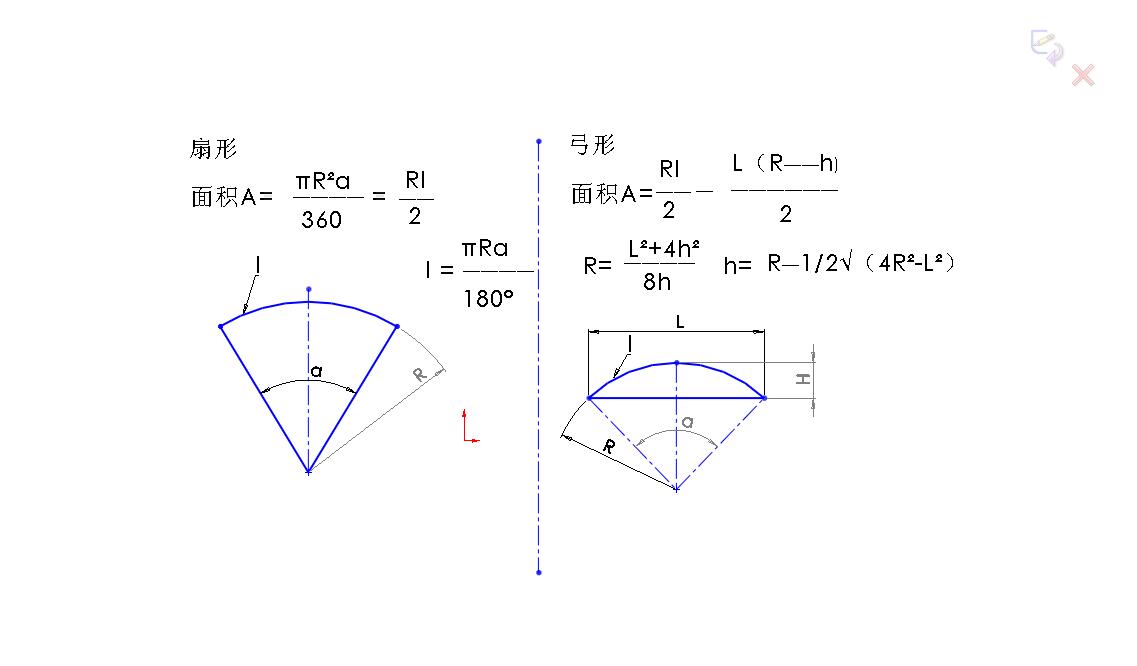
虽然圆的面积公式看似简单，但实际应用中，我们可能会遇到各种不同形状的圆，例如半圆、扇形、环形等等。这些形状的面积计算，都需要在πr²的基础上进行一定的变形和推导。

对于半圆，其面积就是圆面积的一半，即(1/2)πr²。对于扇形，其面积计算需要考虑圆心角的大小，公式为(θ/360°)πr²，其中θ代表圆心角的度数。而对于环形，其面积计算则需要先计算外圆面积和内圆面积，然后相减得到环形的面积，即πR² - πr²，其中R代表外圆半径，r代表内圆半径。

此外，在实际应用中，我们还会遇到一些不规则形状的圆，例如由于磨损或者其他因素导致形状不规则的圆形零件。这时，我们就需要借助一些近似计算的方法，例如将不规则的圆分割成多个规则的小块，分别计算面积，然后求和。

还有一些更复杂的计算方法，比如利用数值积分方法，可以更加精确的计算出不规则图形的面积，这些方法往往需要借助计算机进行计算。

总之，掌握了基本公式并理解其推导过程，我们就能应对大多数圆形面积计算问题。

圆的面积计算在实际生活中的应用：案例分析

• 计算披萨的面积：假设一个披萨的直径为30厘米，那么它的半径为15厘米，面积为π*(15cm)²≈706.86平方厘米。
• 计算水池的面积：假设一个圆形水池的半径为5米，那么它的面积为π*(5m)²≈78.54平方米。
• 计算车轮行驶距离：已知车轮的周长，我们可以根据其半径计算车轮的面积，进而估算车轮行驶的距离。
• 园林绿化设计：在园林绿化设计中，经常需要计算圆形花坛、草坪等的面积，以确定种植面积、用料数量等。
• 工程测量：在工程测量中，圆的面积计算常用于估算土地面积、建筑面积等。

圆的面积计算中可能遇到的问题及解决方法

在实际应用中，计算圆的面积可能会遇到一些问题，例如数据不准确、计算方法选择不当等。

首先，数据的不准确可能会导致计算结果的误差。例如，如果测量圆的半径时存在误差，那么计算出的面积也会存在误差。为了减少误差，我们需要尽可能精确地测量圆的半径。可以使用更精确的测量工具，例如游标卡尺或激光测距仪。多次测量取平均值也是一种常用的方法。

其次，选择不当的计算方法也可能导致计算结果的错误。对于形状规则的圆，直接使用公式πr²即可。但对于形状不规则的圆，则需要选择合适的近似计算方法，例如蒙特卡罗方法或数值积分方法。

另外，还需要注意单位的统一。在计算过程中，要确保所有数据的单位都是一致的，例如都是厘米或都是米，否则计算结果会出错。

最后，对于一些复杂的计算，可以使用计算机软件进行辅助计算，可以提高计算效率和精度。

总而言之，只要我们认真细致地进行测量和计算，选择合适的方法，就可以准确地计算出圆的面积。

圆的面积计算的未来发展趋势：技术与应用

随着科技的进步，圆的面积计算方法也在不断发展和完善。在未来，可能会出现更加精确、高效的计算方法。例如，人工智能技术可以帮助我们更快速、准确地识别和测量圆的形状和大小，从而提高计算效率和精度。

同时，随着计算机技术的发展，三维建模和计算机辅助设计技术可以对不规则形状的圆进行更精确的计算和分析，这将会在建筑、工程等领域发挥重要作用。

在教育方面，未来将会有更多更有效的教学方法，帮助学生更好地理解和掌握圆的面积计算方法。例如，利用虚拟现实技术和增强现实技术，可以将抽象的数学概念转化为更加生动直观的图像，从而提高学生的学习兴趣和理解能力。

此外，随着大数据技术的发展，我们可以收集和分析大量的圆的面积计算数据，建立更完善的数学模型，从而更好地理解和预测圆的面积计算结果。这对于科学研究和实际应用都有着重要的意义。