正方形的面积怎么算？详解公式、应用及进阶知识

本文详细阐述了正方形的面积怎么算，从公式推导到实际应用，再到单位换算和公式拓展，层层递进地讲解了正方形面积计算的各个方面。文章结合生活实例，如瓷砖铺设、土地面积计算等，帮助读者更好地理解和运用正方形面积计算公式。希望读者通过学习本文，能够熟练掌握正方形面积的计算方法，并能够将其应用到实际生活中，解决各种相关的实际问题，例如计算不规则图形的面积。

正方形面积计算公式及推导

正方形的面积计算，是几何学中最基础也是最重要的内容之一。其核心公式简洁明了：面积 = 边长 × 边长，或写作 S = a² ，其中 S 代表面积，a 代表正方形的边长。

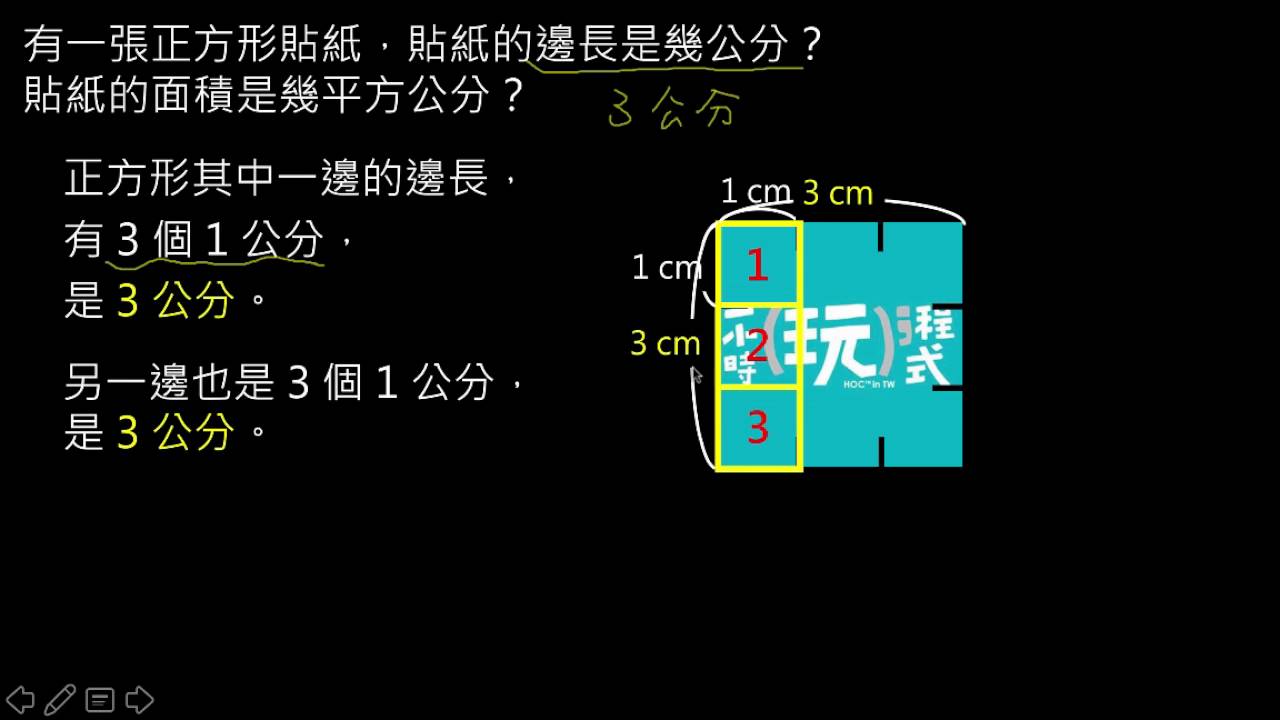
这个公式的推导可以基于小学阶段学习的面积概念。我们可以将一个正方形分割成若干个小正方形，然后通过数小正方形的个数来求得总面积。例如，一个边长为 2 厘米的正方形，可以分割成 4 个边长为 1 厘米的小正方形，总面积为 4 平方厘米。以此类推，我们可以得出正方形面积等于边长的平方这一结论。

理解公式的推导过程，能够帮助我们更深刻地掌握正方形面积计算的原理。 在实际应用中，我们可以灵活运用此公式解决各种问题。例如，计算一块边长为 5 米的正方形土地的面积，只需要将 5 代入公式即可，面积为 25 平方米。 根据公开资料显示，在小学数学教学中，正方形面积的计算是重要的学习内容，能够帮助学生建立几何计算的基本概念。

正方形面积计算在实际生活中的应用

正方形面积的计算并非仅仅局限于课堂理论，它在实际生活中有着广泛的应用。从日常生活到工程建设，都能见到它的身影。

例如，在装修房屋时，需要计算瓷砖的用量。假设房间地面铺设的瓷砖为边长 30 厘米的正方形瓷砖，我们需要计算房间地面面积，才能知道需要多少块瓷砖。如果房间地面是一个边长为 3 米的正方形，那么地面面积为 9 平方米，也就是 90000 平方厘米。每块瓷砖的面积为 900 平方厘米，所以需要 100 块瓷砖。

另一个例子是农业生产。农民在耕种土地时，也常常需要计算土地面积。假设一个农田是一个边长为 10 米的正方形，那么农田面积为 100 平方米。根据相关研究表明，精确计算土地面积，对于合理规划种植方案、提高农作物产量至关重要。 在这些实际应用中，准确的正方形面积计算至关重要，这凸显了学习掌握这个基础几何知识的实用性。

不同单位下的正方形面积换算

在进行正方形面积计算时，我们常常会遇到不同单位的换算问题。例如，边长用米计算，面积则用平方米计算；边长用厘米计算，面积则用平方厘米计算。

单位换算需要特别注意。1 平方米等于 10000 平方厘米，1 平方厘米等于 0.0001 平方米。 在实际计算中，我们需要根据实际情况选择合适的单位，并进行相应的单位换算，确保计算结果的准确性。

例如，如果一个正方形边长是 1.5 米，那么它的面积是 2.25 平方米。如果将边长换算成厘米（1.5 米 = 150 厘米），那么面积就应该是 22500 平方厘米。两者数值虽然不同，但单位不同，计算结果是等效的。在工程测量中，单位换算的精确性直接关系到工程的质量与成本，因此需要格外谨慎。

正方形面积计算公式的拓展与延伸

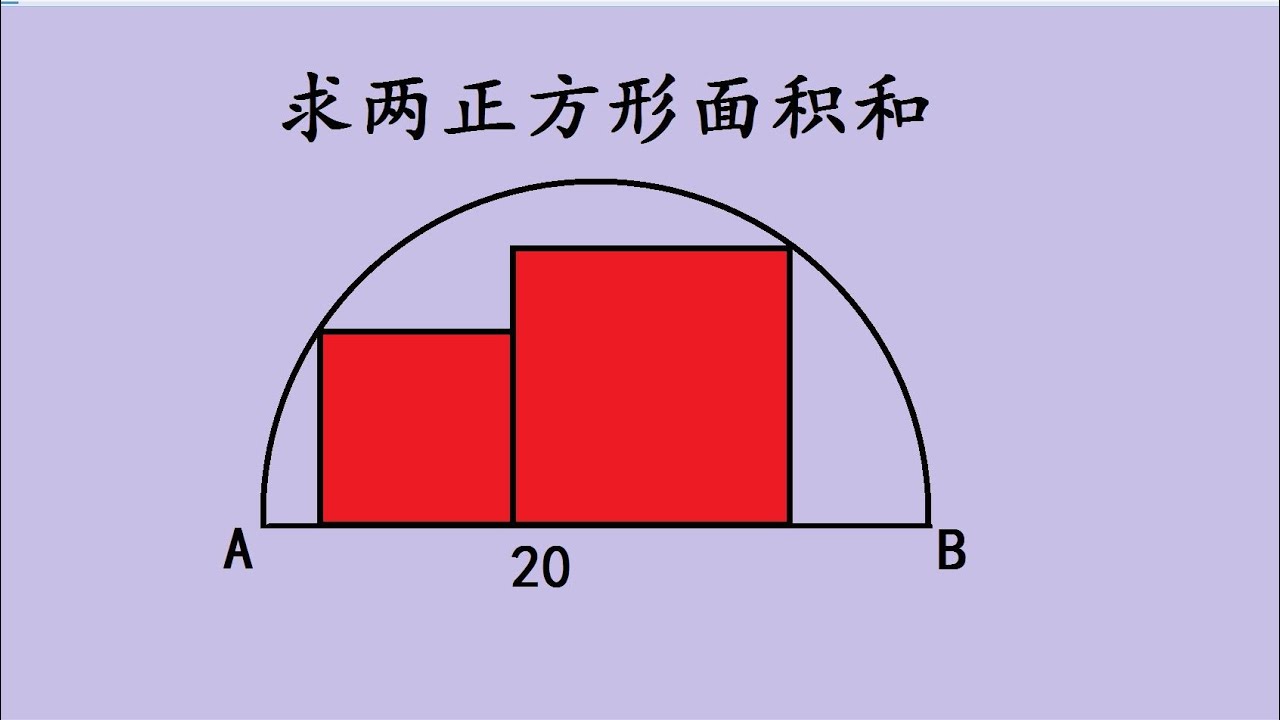
正方形面积计算公式 S = a² 是一个基础公式，但它可以被拓展和延伸到更复杂的几何图形计算中。例如，我们可以利用这个公式计算正方形的内切圆或外接圆的面积。

通过几何关系的推导，我们可以发现，正方形的内切圆直径等于正方形边长，而外接圆直径等于正方形的对角线。利用圆的面积公式 S = πr² (其中 r 为半径)，我们可以轻松计算出正方形内切圆和外接圆的面积。

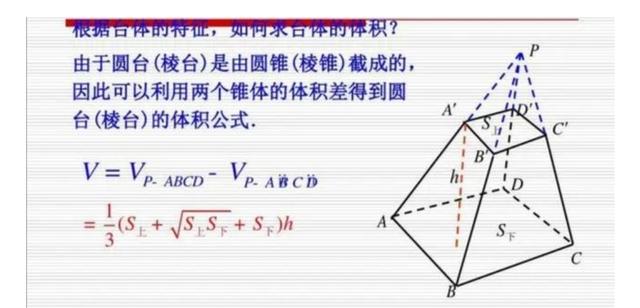
正方形面积的计算还可以应用于更复杂的平面图形的面积计算中。许多不规则图形可以分解成若干个正方形和其它简单图形，再利用相应的公式进行计算。学习这些拓展与延伸知识，不仅能够加深我们对正方形面积公式的理解，也能够提高我们解决更复杂几何问题的能力，这在高等数学及工程计算中非常重要。